Question

【题目】如图，在棱长为1的正方体ABCD﹣A1B1C1D1的对角线AC1上任取一点P，以A为球心，AP为半径作一个球．设AP=x，记该球面与正方体表面的交线的长度和为f（x），则函数f（x）的图象最有可能的是（ ）

A.
B.
C.
D.

Answer 1

【答案】B
【解析】解：如图，球面与正方体的表面都相交，
根据选项的特点，我们考虑三个特殊情形：①当x=1；②当x= ；③当x= ．
①当x=1时，以A为球心，1为半径作一个球，该球面与正方体表面的交线分别是图中的红色的弧线，其弧长为：3× ×2π×1= ，且为函数f（x）的最大值；
②当x= 时，以A为球心， 为半径作一个球，该球面与正方体表面的交线分别是图中的兰色的弧线，根据图形的相似，其弧长为①中弧长的一半；
③当x= ．以A为球心， 为半径作一个球，该球面与正方体表面的交线分别是图中的粉红色的弧线，其弧长为：3× ×2π×1= ，且为函数f（x）的最大值；
对照选项，B正确．
故选B．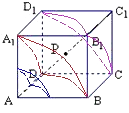

【考点精析】认真审题，首先需要了解棱柱的结构特征(两底面是对应边平行的全等多边形；侧面、对角面都是平行四边形；侧棱平行且相等；平行于底面的截面是与底面全等的多边形)．