
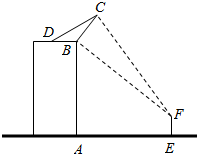
 ��ͼ��һ¥����ABΪ19$\sqrt{3}$�ף�ij��湫˾��¥����װһ���BCΪ4�Ĺ���ƣ�CDΪ���ˣ�����Ƶ����Ϊ60�㣬��װ�����У�һ����Ϊ$\sqrt{3}$�ļ�����ԱEFվ��¥ǰ�۲�ù㴫�Ƶİ�װЧ����Ϊ��֤��ȫ���ü�����Ա����վ�ڹ���Ƶ����·�����AE=x�ף��ü�����Ա�۲����Ƶ��ӽǡ�BFC=�ȣ�
��ͼ��һ¥����ABΪ19$\sqrt{3}$�ף�ij��湫˾��¥����װһ���BCΪ4�Ĺ���ƣ�CDΪ���ˣ�����Ƶ����Ϊ60�㣬��װ�����У�һ����Ϊ$\sqrt{3}$�ļ�����ԱEFվ��¥ǰ�۲�ù㴫�Ƶİ�װЧ����Ϊ��֤��ȫ���ü�����Ա����վ�ڹ���Ƶ����·�����AE=x�ף��ü�����Ա�۲����Ƶ��ӽǡ�BFC=�ȣ����� ��1��ͨ����CG��AE��G����FH��AB��H����CG��M����BN��CG��N�����=��CFM-��BFH��������ǵ����еĶ����֪��Rt��CFM��tan��CFM=$\frac{20\sqrt{3}}{x-2}$����Rt��BFH��tan��BFH=$\frac{18\sqrt{3}}{x}$�����ò�ǵ����й�ʽ���㼴�ý��ۣ�
��2��ͨ����1����֪��tan��=$2\sqrt{3}$•$\frac{x+18}{{x}^{2}-2x+1080}$��ͨ����t=x+18����Ԫ�����֪tan��=$\frac{2\sqrt{3}}{t+\frac{1440}{t}-38}$���������û�������ʽ���㼴�ý��ۣ�
��� 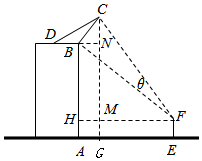 �⣺��1����CG��AE��G����FH��AB��H����CG��M��
�⣺��1����CG��AE��G����FH��AB��H����CG��M��
��BN��CG��N�����=��CFM-��BFH��
��Rt��BCN�У�BC=4����CBN=60�㣬��BN=2��CN=2$\sqrt{3}$��
��Rt��CFM����tan��CFM=$\frac{CM}{MF}$=$\frac{CN+NM}{AE-BN}$=$\frac{20\sqrt{3}}{x-2}$��
��Rt��BFH����tan��BFH=$\frac{BH}{HF}$=$\frac{18\sqrt{3}}{x}$��
��tan��=tan����CFM-BFH��=$\frac{tan��CFM-tan��BFH}{1+tan��CFM•tan��BFH}$
=$\frac{\frac{20\sqrt{3}}{x-2}-\frac{18\sqrt{3}}{x}}{1+\frac{20\sqrt{3}}{x-2}•\frac{18\sqrt{3}}{x}}$=$\frac{2\sqrt{3}x+36\sqrt{3}}{{x}^{2}-2x+1080}$��
�����⣬������Աֻ����G���Ҳ࣬��x�ʣ�2��+�ޣ���
��2���ɣ�1����֪��tan��=$\frac{2\sqrt{3}x+36\sqrt{3}}{{x}^{2}-2x+1080}$=$2\sqrt{3}$•$\frac{x+18}{{x}^{2}-2x+1080}$��
��t=x+18����t�ʣ�20��+�ޣ���
��tan��=$2\sqrt{3}$•$\frac{t}{��t-18��^{2}-2��t-18��+1080}$=$\frac{2\sqrt{3}}{t+\frac{1440}{t}-38}$��$\frac{\sqrt{3}}{12\sqrt{10}-19}$��
���ҽ���t=$\frac{1440}{t}$��t=$12\sqrt{10}$ʱȡ�Ⱥţ���ʱ��x=$12\sqrt{10}$-18��
�֡ߦ�Ϊ��ǣ�y=tan�������䣨0��$\frac{��}{2}$���ϵ���������
�൱x=$12\sqrt{10}$-18ʱ����ȡ�����ֵ��
���� ���⿼����һ�����ں������ۺ�Ӧ���⣬����������⡢�������������������������������ע����ⷽ���Ļ��ۣ��������⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{2}{3}$ | B�� | -$\frac{2}{3}$ | C�� | $\frac{3}{2}$ | D�� | -$\frac{3}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [$\sqrt{5}-4$��$\sqrt{5}+4$] | B�� | ��-�ޣ�-5] | C�� | [-5��+�ޣ� | D�� | ��-�ޣ�-5�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{5}{2}$ | B�� | 2 | C�� | -$\frac{1}{2}$ | D�� | -3 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com