
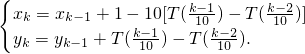 .其中T(a)表示非负实数a的整数部分,如T(2.7)=2,T(0.3)=0.按此方案,第2011棵树种植点的坐标是________.
.其中T(a)表示非负实数a的整数部分,如T(2.7)=2,T(0.3)=0.按此方案,第2011棵树种植点的坐标是________.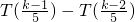 成的数列为1,0,0,0,0,1,0,0,0,0,1,0,0,0,0,1…,k=1,2,3,4,5,…一一代入计算得数列{xn}为1,2,3,4,5,1,2,3,4,5,1,2,3,4,5,…即{xn}是以5为周期的周期数列,从而有x5n+1=1,x5n+2=2,x5n+3=3,x5n+4=4,x5n=5.n∈N*.
成的数列为1,0,0,0,0,1,0,0,0,0,1,0,0,0,0,1…,k=1,2,3,4,5,…一一代入计算得数列{xn}为1,2,3,4,5,1,2,3,4,5,1,2,3,4,5,…即{xn}是以5为周期的周期数列,从而有x5n+1=1,x5n+2=2,x5n+3=3,x5n+4=4,x5n=5.n∈N*.

 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:解答题
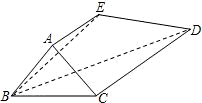 多面体ABCDE中,AB=BC=AC=AE=1,CD=2,AE⊥面ABC,AE∥CD.
多面体ABCDE中,AB=BC=AC=AE=1,CD=2,AE⊥面ABC,AE∥CD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com