
【题目】已知一工厂生产了某种产品700件,该工厂对这些产品进行了安全和环保这两个性能的质量检测。工厂决定利用随机数表法从中抽取100件产品进行抽样检测,现将700件产品按001,002,…,700进行编号;
(1)如果从第8行第4列的数开始向右读,请你依次写出最先检测的3件产品的编号;
(下面摘取了随机数表的第7~9行)
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76
63 01 63 78 59 16 95 55 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 79
33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54
(2)抽取的100件产品的安全性能和环保性能的质量检测结果如下表:
检测结果分为优等、合格、不合格三个等级,横向和纵向分别表示安全性能和环保性能。若在该样本中,产品环保性能是优等的概率为![]() ,求
,求![]() ,
,![]() 的值。
的值。
件数 | 环保性能 | |||
优等 | 合格 | 不合格 | ||
安全性能 | 优等 | 6 | 20 | 5 |
合格 | 10 | 18 | 6 | |
不合格 |
| 4 |
| |
(3)已知![]() ,
,![]() ,求在安全性能不合格的产品中,环保性能为优等的件数比不合格的件数少的概率。
,求在安全性能不合格的产品中,环保性能为优等的件数比不合格的件数少的概率。
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:高中数学 来源: 题型:
【题目】通过随机询问某地100名高中学生在选择座位时是否挑同桌,得到如下![]() 列联表:
列联表:
男生 | 女生 | 合计 | |
挑同桌 | 30 | 40 | 70 |
不挑同桌 | 20 | 10 | 30 |
总计 | 50 | 50 | 100 |
![]() Ⅰ
Ⅰ![]() 从这50名男生中按是否挑同桌采取分层抽样的方法抽取一个容量为5的样本,现从这5人中随机选取3人做深度采访,求这3名学生中至少有2名要挑同桌的概率;
从这50名男生中按是否挑同桌采取分层抽样的方法抽取一个容量为5的样本,现从这5人中随机选取3人做深度采访,求这3名学生中至少有2名要挑同桌的概率;
![]() Ⅱ
Ⅱ![]() 根据以上
根据以上![]() 列联表,是否有
列联表,是否有![]() 以上的把握认为“性别与在选择座位时是否挑同桌”有关?
以上的把握认为“性别与在选择座位时是否挑同桌”有关?
下面的临界值表供参考:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() 参考公式:
参考公式: ![]() ,其中
,其中![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() x2+alnx.
x2+alnx.
(1)若a=﹣1,求函数f(x)的极值,并指出极大值还是极小值;
(2)若a=1,求函数f(x)在[1,e]上的最值;
(3)若a=1,求证:在区间[1,+∞)上,函数f(x)的图象在g(x)=![]() x3的图象下方.
x3的图象下方.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中华人民共和国道路交通安全法》第47条的相关规定:机动车行经人行横道时,应当减速慢行;遇行人正在通过人行横道,应当停车让行,俗称“礼让斑马线”,《中华人民共和国道路交通安全法》 第90条规定:对不礼让行人的驾驶员处以扣3分,罚款50元的处罚.下表是某市一主干路口监控设备所抓拍的5个月内驾驶员不“礼让斑马线”行为统计数据:
月份 | 1 | 2 | 3 | 4 | 5 |
违章驾驶员人数 | 120 | 105 | 100 | 90 | 85 |
(1)请利用所给数据求违章人数y与月份之间的回归直线方程![]() +
+![]()
(2)预测该路口7月份的不“礼让斑马线”违章驾驶员人数;
(3)交警从这5个月内通过该路口的驾驶员中随机抽查了50人,调查驾驶员不“礼让斑马线”行为与驾龄的关系,得到如下2![]() 列联表:
列联表:
不礼让斑马线 | 礼让斑马线 | 合计 | |
驾龄不超过1年 | 22 | 8 | 30 |
驾龄1年以上 | 8 | 12 | 20 |
合计 | 30 | 20 | 50 |
能否据此判断有97.5![]() 的把握认为“礼让斑马线”行为与驾龄有关?
的把握认为“礼让斑马线”行为与驾龄有关?
参考公式及数据: ,
,![]() .
.
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() (其中n=a+b+c+d)
(其中n=a+b+c+d)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°.
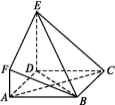
(1)求二面角F-BE-D的余弦值;
(2)设点M是线段BD上一个动点,试确定点M的位置,使得AM∥平面BEF,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的右顶点为A,上顶点为B.已知椭圆的离心率为
的右顶点为A,上顶点为B.已知椭圆的离心率为![]() ,
,![]() .
.
(1)求椭圆的方程;
(2)设直线![]() 与椭圆交于
与椭圆交于![]() ,
,![]() 两点,
两点,![]() 与直线
与直线![]() 交于点M,且点P,M均在第四象限.若
交于点M,且点P,M均在第四象限.若![]() 的面积是
的面积是![]() 面积的2倍,求
面积的2倍,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法错误的是
A. 对分类变量X与Y,随机变量K2的观测值k越大,则判断“X与Y有关系”的把握程度越小
B. 在回归直线方程![]() =0.2x+0.8中,当解释变量x每增加1个单位时,预报变量
=0.2x+0.8中,当解释变量x每增加1个单位时,预报变量![]() 平均增加0.2个单位
平均增加0.2个单位
C. 两个随机变量的线性相关性越强,则相关系数的绝对值就越接近于1
D. 回归直线过样本点的中心(![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() (限定
(限定![]() ).
).
(1)写出曲线![]() 的极坐标方程,并求
的极坐标方程,并求![]() 与
与![]() 交点的极坐标;
交点的极坐标;
(2)射线![]() 与曲线
与曲线![]() 与
与![]() 分别交于点
分别交于点![]() (
(![]() 异于原点),求
异于原点),求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com