Question

在正方体ABCD-A₁B₁C₁D₁中，点M、N分别在AB₁、BC₁上，且AM=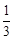AB₁，BN=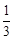BC₁，则下列结论：①AA₁⊥MN；②A₁C₁// MN；③MN//平面A₁B₁C₁D₁；④B₁D₁⊥MN，其中，

正确命题的个数是（  ）

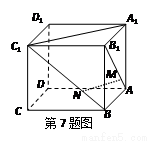
     A．1             B．2             C．3               D．4

 

Answer 1

【答案】

B

【解析】解；在正方体ABCD-A₁B₁C₁D₁的四条棱A₁A，B₁B，C₁C，D₁D上分别取点G，F，E，H四点，

使AG=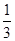 A₁A，BF=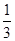B₁B，CE=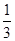C₁C，DH= 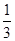D₁D，连接GF，FE，EH，HG，

∵点M、N分别在AB₁、BC₁上，且AM=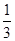AB₁，BN= 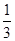BC₁，

∴M在线段GF上，N点在线段FE上．且四边形GFEH为正方形，平面GFEH∥平面A₁B₁C₁D₁，

∵AA₁⊥平面A₁B₁C₁D₁，∴AA₁⊥平面GFEH，∵MN⊂平面GFEH，∴AA₁⊥MN，∴①正确．

∵A₁C₁∥GE，而GE与MN不平行，∴A₁C₁与MN不平行，∴②错误．

∵平面GFEH∥平面A₁B₁C₁D₁，MN⊂平面GFEH，∴MN∥平面A₁B₁C₁D₁，∴③正确．

∵B₁D₁⊥FH，FH⊂平面GFEH，MN⊂平面GFEH，B₁D₁⊂平面A₁B₁C₁D₁，平面GFEH∥平面A₁B₁C₁D₁，

且MN与FH不平行，∴B₁D₁不可能垂直于MN，∴④错误

∴正确命题只有①③

故选B