
【题目】设![]() ,
,![]() ,其中m是不等于零的常数,
,其中m是不等于零的常数,
(1)![]() 时,直接写出
时,直接写出![]() 的值域;
的值域;
(2)求![]() 的单调递增区间;
的单调递增区间;
(3)已知函数![]() (
(![]() ),定义:
),定义:![]() (
(![]() ),
),![]() (
(![]() ).其中,
).其中,![]() 表示函数
表示函数![]() 在D上的最小值,
在D上的最小值,![]() 表示函数
表示函数![]() 在D上的最大值.例如:
在D上的最大值.例如:![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() .当
.当![]() 时,设
时,设![]() ,不等式
,不等式![]() 恒成立,求t,n的取值范围;
恒成立,求t,n的取值范围;
【答案】(1)![]() ;(2)
;(2)![]() 时,
时,![]() 在
在![]() 递增;
递增;![]() 时,
时,![]() 在
在![]() 递增
递增![]() 时,
时,![]() 在
在![]() 递增(3)
递增(3)![]() ,
,![]()
【解析】
(1)将![]() 代入函数
代入函数![]() 的表达式中,运用函数单调性直接得到函数
的表达式中,运用函数单调性直接得到函数![]() 的值域.
的值域.
(2)运用导数先对函数![]() 求导,然后分类讨论
求导,然后分类讨论![]() 的值,在不同情况下得到函数
的值,在不同情况下得到函数![]() 的单调递增区间
的单调递增区间
(3)阅读题意,结合题中所给的信息,先表示出![]() 的表达式,然后再求出
的表达式,然后再求出![]() 和
和![]() ,最后化简出不等式
,最后化简出不等式![]() ,解不等式恒成立的情况得到结果
,解不等式恒成立的情况得到结果
(1)当![]() 时,
时, ![]() ,
,![]() ,所以
,所以![]() 的值域为
的值域为![]() ,综上
,综上![]() .
.
(2)因为![]() ,所以
,所以![]() ,
,
当![]() 时,
时, ![]() ,则
,则![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,令
时,令![]() ,解得
,解得![]() ,
,
若![]() ,即
,即![]() 时,
时, ![]() 恒成立, 则
恒成立, 则![]() 在
在![]() 上单调递增;
上单调递增;
若![]() ,即
,即![]() 时,令
时,令![]() ,解得
,解得![]() ,则
,则![]() 在
在![]() 上单调递增.
上单调递增.
综上, ![]() 时,
时,![]() 在
在![]() 递增;
递增;![]() 时,
时,![]() 在
在![]() 递增
递增![]() 时,
时,![]() 在
在![]() 递增.
递增.
(3)由题意得, 当![]() 时,
时,![]() ,
,![]() ,
,
则![]() ,
,![]() ,令
,令![]() 解得
解得![]() ;令
;令![]() 解得
解得![]() ;令
;令![]() 解得
解得![]() ,化简
,化简![]() 得
得
![]() 即
即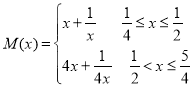 ,结合题意计算可得
,结合题意计算可得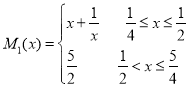 ;
;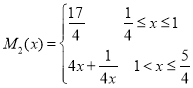 ;计算
;计算![]() 得
得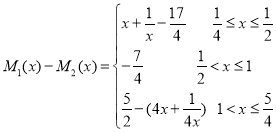 ;可得
;可得![]() ,又因为
,又因为![]() 恒成立,所以
恒成立,所以![]() ,
,![]() .
.
综上![]() ,
,![]()


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的左右焦点分别为
的左右焦点分别为![]() ,短轴两个端点为
,短轴两个端点为![]() ,且四边形
,且四边形![]() 是边长为2的正方形.
是边长为2的正方形.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 是椭圆
是椭圆![]() 上一点,
上一点,![]() 为椭圆长轴上一点,求
为椭圆长轴上一点,求![]() 的最大值与最小值;
的最大值与最小值;
(3)设![]() 是椭圆
是椭圆![]() 外的动点,满足
外的动点,满足![]() ,点
,点![]() 是线段
是线段![]() 与该椭圆的交点,点
与该椭圆的交点,点![]() 在线段
在线段![]() 上,并且满足
上,并且满足![]() ,
,![]() ,求点
,求点![]() 的轨迹方程.
的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知无穷数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足![]() ,其中
,其中![]() 、
、![]() 、
、![]() 是常数.
是常数.
(1)若![]() ,
,![]() ,
,![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2)若![]() ,
,![]() ,
,![]() ,且
,且![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)试探究![]() 、
、![]() 、
、![]() 满足什么条件时,数列
满足什么条件时,数列![]() 是公比不为
是公比不为![]() 的等比数列.
的等比数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,圆![]() 与长轴是短轴两倍的椭圆
与长轴是短轴两倍的椭圆![]() :
:![]() 相切于点
相切于点![]()
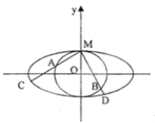
(1)求椭圆![]() 与圆
与圆![]() 的方程;
的方程;
(2)过点![]() 引两条互相垂直的两直线
引两条互相垂直的两直线![]() 与两曲线分别交于点
与两曲线分别交于点![]() 与点
与点![]() (均不重合).若
(均不重合).若![]() 为椭圆上任一点,记点
为椭圆上任一点,记点![]() 到两直线的距离分别为
到两直线的距离分别为![]() ,求
,求![]() 的最大值,并求出此时
的最大值,并求出此时![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (
(![]() )的焦距为
)的焦距为![]() ,且右焦点F与短轴的两个端点组成一个正三角形.若直线l与椭圆C交于
,且右焦点F与短轴的两个端点组成一个正三角形.若直线l与椭圆C交于![]() 、
、![]() ,且在椭圆C上存在点M,使得:
,且在椭圆C上存在点M,使得:![]() (其中O为坐标原点),则称直线l具有性质H.
(其中O为坐标原点),则称直线l具有性质H.
(1)求椭圆C的方程;
(2)若直线l垂直于x轴,且具有性质H,求直线l的方程;
(3)求证:在椭圆C上不存在三个不同的点P、Q、R,使得直线![]() 、
、![]() 、
、![]() 都具有性质H.
都具有性质H.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() .
.
(1)求出![]() ,
,![]() ,
,![]() 的值,并求出
的值,并求出![]() 及数列
及数列![]() 的通项公式;
的通项公式;
(2)设![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)设![]() ,在数列
,在数列![]() 中取出
中取出![]() (
(![]() 且
且![]() )项,按照原来的顺序排列成一列,构成等比数列
)项,按照原来的顺序排列成一列,构成等比数列![]() ,若对任意的数列
,若对任意的数列![]() ,均有
,均有![]() ,试求
,试求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】福彩是利国利民游戏,其刮刮乐之《蓝色奇迹》:如图(1)示例,刮开票面看到最左侧一列四个两位数字为“我的号码”,最上行四个两位数为“中奖号码”,这八个两位数是00至99这一百个数字随机产生的,若两个数字相同即中得其相交线上的奖金,奖金可以累加.小明买的一张《蓝色奇迹》刮刮乐如图(2),除了一个“我的号码”外,他已经刮开票面上其它所有数字,依据目前的信息,小明从这张刮刮乐得到的奖金额高于600元的概率为(无所得税)( )


图(1) 图(2)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com