
【题目】将两颗正方体型骰子投掷一次,则向上的点数之和是![]() 的概率为_____,向上的点数之和不小于
的概率为_____,向上的点数之和不小于![]() 的概率为_____.
的概率为_____.
【答案】![]()
![]()
【解析】
(1)利用古典概型的概率公式求解;(2)求出所有的基本事件和向上的点数之和不小于![]() 的基本事件的数量,再利用古典概型的概率公式即得解.
的基本事件的数量,再利用古典概型的概率公式即得解.
(1)将两颗正方体型骰子投掷一次,共有6×6=36个结果,其中向上的点数之和是10的基本事件有(4,6),(5,5),(6,4),共3种,由古典概型的概率公式得向上的点数之和是![]() 的概率为
的概率为![]() .
.
(2) 将两颗正方体型骰子投掷一次,共有6×6=36个结果,其中向上的点数之和不小于10的基本事件有(4,6),(5,5),(6,4),(5,6),(6,5),(6,6),共6种,由古典概型的概率公式得向上的点数之和不小于![]() 的概率为
的概率为![]() .
.
故答案为:(1). ![]() (2).
(2). ![]()


科目:高中数学 来源: 题型:
【题目】已知中心在原点,焦点在x轴上的椭圆C的离心率为![]() ,且经过点M(1,
,且经过点M(1,![]() ),过点P(2,1)的直线l与椭圆C相交于不同的两点A,B.
),过点P(2,1)的直线l与椭圆C相交于不同的两点A,B.
(1)求椭圆C的方程;
(2)是否存在直线l,满足![]() ?若存在,求出直线l的方程;若不存在,请说明理由.
?若存在,求出直线l的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数集![]() (
(![]() ,
,![]() )具有性质P;对任意的i,j(
)具有性质P;对任意的i,j(![]() ),
),![]() 与
与![]() 两数中至少有一个属于A.
两数中至少有一个属于A.
(1)分别判断数集![]() 与
与![]() 是否具有性质P,并说明理由;
是否具有性质P,并说明理由;
(2)证明:![]() ,且
,且![]() ;
;
(3)当![]() 时,若
时,若![]() ,求集合A.
,求集合A.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (a∈R).
(a∈R).
(1)若曲线y=f(x)在x=e处切线的斜率为﹣1,求此切线方程;
(2)若f(x)有两个极值点x1,x2,求a的取值范围,并证明:x1x2>x1+x2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三有500名学生,在一次考试的英语成绩服从正态分布![]() ,数学成绩的频率分布直方图如下:
,数学成绩的频率分布直方图如下:
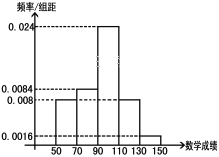
(Ⅰ)如果成绩大于135的为特别优秀,则本次考试英语、数学特别优秀的大约各多少人?
(Ⅱ)试问本次考试英语和数学的成绩哪个较高,并说明理由.
(Ⅲ)如果英语和数学两科都特别优秀的共有6人,从(Ⅰ)中的这些同学中随机抽取3人,设三人中两科都特别优秀的有![]() 人,求
人,求![]() 的分布列和数学期望。
的分布列和数学期望。
参考公式及数据:
若![]() ,则
,则![]() ,
,
![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 和
和![]() 都是定义在集合
都是定义在集合![]() 上的函数,对于任意的
上的函数,对于任意的![]() ,都有
,都有![]() 成立,称函数
成立,称函数![]() 与
与![]() 在
在![]() 上互为“互换函数”.
上互为“互换函数”.
(1)函数![]() 与
与![]() 在
在![]() 上互为“互换函数”,求集合
上互为“互换函数”,求集合![]() ;
;
(2)若函数![]() (
(![]() 且
且![]() )与
)与![]() 在集合
在集合![]() 上互为“互换函数”,求证:
上互为“互换函数”,求证:![]() ;
;
(3)函数![]() 与
与![]() 在集合
在集合![]() 且
且![]() 上互为“互换函数”,当
上互为“互换函数”,当![]() 时,
时,![]() ,且
,且![]() 在
在![]() 上是偶函数,求函数
上是偶函数,求函数![]() 在集合
在集合![]() 上的解析式.
上的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com