
【题目】已知函数![]() 在
在![]() 处的切线方程为
处的切线方程为![]() .
.
(1)求![]() 的值;
的值;
(2)记![]() ,求函数
,求函数![]() 在
在![]() 上的最小值;
上的最小值;
(3)若对任意的![]() ,恒有
,恒有![]() ,求
,求![]() 的取值范围.
的取值范围.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】设等差数列![]() 的首项为0,公差为a,
的首项为0,公差为a,![]() ;等差数列
;等差数列![]() 的首项为0,公差为b,
的首项为0,公差为b,![]() .由数列
.由数列![]() 和
和![]() 构造数表M,与数表
构造数表M,与数表![]() ;
;
记数表M中位于第i行第j列的元素为![]() ,其中
,其中![]() ,(i,j=1,2,3,…).
,(i,j=1,2,3,…).
记数表![]() 中位于第i行第j列的元素为
中位于第i行第j列的元素为![]() ,其中
,其中![]() (
(![]() ,
,![]() ,
,![]() ).如:
).如:![]() ,
,![]() .
.
(1)设![]() ,
,![]() ,请计算
,请计算![]() ,
,![]() ,
,![]() ;
;
(2)设![]() ,
,![]() ,试求
,试求![]() ,
,![]() 的表达式(用i,j表示),并证明:对于整数t,若t不属于数表M,则t属于数表
的表达式(用i,j表示),并证明:对于整数t,若t不属于数表M,则t属于数表![]() ;
;
(3)设![]() ,
,![]() ,对于整数t,t不属于数表M,求t的最大值.
,对于整数t,t不属于数表M,求t的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,焦距为
,焦距为![]() .斜率为k的直线l与椭圆M有两个不同的交点A,B.
.斜率为k的直线l与椭圆M有两个不同的交点A,B.
(Ⅰ)求椭圆M的方程;
(Ⅱ)若![]() ,求
,求![]() 的最大值;
的最大值;
(Ⅲ)设![]() ,直线PA与椭圆M的另一个交点为C,直线PB与椭圆M的另一个交点为D.若C,D和点
,直线PA与椭圆M的另一个交点为C,直线PB与椭圆M的另一个交点为D.若C,D和点![]() 共线,求k.
共线,求k.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】今年是新中国成立70周年.70年来,在中国共产党的坚强领导下,全国各族人民团结心,迎难而上,开拓进取,奋力前行,创造了一个又一个人类发展史上的伟大奇迹,中华民族迎来了从站起来、富起来到强起来的伟大飞跃.某公司统计了第![]() 年(2013年是第一年)的经济效益为
年(2013年是第一年)的经济效益为![]() (千万元),得到如下表格:
(千万元),得到如下表格:
| 3 | 4 | 5 | 6 |
| 2.5 | 3 | 4 | 4.5 |
若由表中数据得到![]() 关于
关于![]() 的线性回归方程是
的线性回归方程是![]() ,则可预测2020年经济效益大约是( )
,则可预测2020年经济效益大约是( )
A.5.95千万元B.5.25千万元C.5.2千万元D.5千万元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲和乙两个人计划周末参加志愿者活动,约定在周日早上8:00至8:30之间到某公交站搭乘公交车一起去,已知在这段时间内,共有![]() 班公交车到达该站,到站的时间分别为8:05,8:15,8:30,如果他们约定见车就搭乘,则甲和乙两个人恰好能搭乘同一班公交车去的概率为( )
班公交车到达该站,到站的时间分别为8:05,8:15,8:30,如果他们约定见车就搭乘,则甲和乙两个人恰好能搭乘同一班公交车去的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,已知抛物线C:y2=2px(p>0)的焦点为F,过F垂直于x轴的直线与C相交于A、B两点,△AOB的面积为2.
(1)求抛物线C的方程;
(2)若过P(![]() ,0)的直线与C相交于M,N两点,且
,0)的直线与C相交于M,N两点,且![]() 2
2![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】冬天的北方室外温度极低,若轻薄保暖的石墨烯发热膜能用在衣服上,可爱的医务工作者行动会更方便.石墨烯发热膜的制作:从石墨中分离出石墨烯,制成石墨烯发热膜.从石墨分离石墨烯的一种方法是化学气相沉积法,使石墨升华后附着在材料上再结晶.现在有![]() 材料、
材料、![]() 材料供选择,研究人员对附着在
材料供选择,研究人员对附着在![]() 材料、
材料、![]() 材料上再结晶各做了50次试验,得到如下等高条形图.
材料上再结晶各做了50次试验,得到如下等高条形图.
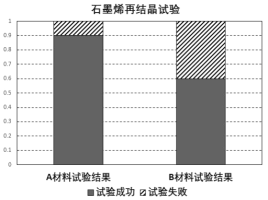
(1)根据上面的等高条形图,填写如下列联表,判断是否有99%的把握认为试验成功与材料有关?
|
| 合计 | |
成功 | |||
不成功 | |||
合计 |
(2)研究人员得到石墨烯后,再制作石墨烯发热膜有三个环节:①透明基底及![]() 胶层;②石墨烯层;③表面封装层.第一、二环节生产合格的概率均为
胶层;②石墨烯层;③表面封装层.第一、二环节生产合格的概率均为![]() ,第三个环节生产合格的概率为
,第三个环节生产合格的概率为![]() ,且各生产环节相互独立.已知生产1吨的石墨烯发热膜的固定成本为1万元,若生产不合格还需进行修复,第三个环节的修复费用为3000元,其余环节修复费用均为1000元.如何定价,才能实现每生产1吨石墨烯发热膜获利可达1万元以上的目标?
,且各生产环节相互独立.已知生产1吨的石墨烯发热膜的固定成本为1万元,若生产不合格还需进行修复,第三个环节的修复费用为3000元,其余环节修复费用均为1000元.如何定价,才能实现每生产1吨石墨烯发热膜获利可达1万元以上的目标?
附:参考公式: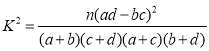 ,其中
,其中![]() .
.
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分10分)选修4—4,坐标系与参数方程
已知曲线![]() ,直线
,直线![]() :
:![]() (
(![]() 为参数).
为参数).
(I)写出曲线![]() 的参数方程,直线
的参数方程,直线![]() 的普通方程;
的普通方程;
(II)过曲线![]() 上任意一点
上任意一点![]() 作与
作与![]() 夹角为
夹角为![]() 的直线,交
的直线,交![]() 于点
于点![]() ,
,![]() 的最大值与最小值.
的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是椭圆
是椭圆![]() 的左右顶点,
的左右顶点,![]() 点为椭圆
点为椭圆![]() 上一点,点
上一点,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,且
,且![]() .
.
(1)若椭圆![]() 经过圆
经过圆![]() 的圆心,求椭圆
的圆心,求椭圆![]() 的方程;
的方程;
(2)在(1)的条件下,若过点![]() 的直线与椭圆
的直线与椭圆![]() 相交于不同的
相交于不同的![]() 两点,设
两点,设![]() 为椭圆
为椭圆![]() 上一点,且满足
上一点,且满足![]() (
(![]() 为坐标原点),当
为坐标原点),当![]() 时,求实数
时,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com