练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】甲、乙两人进行围棋比赛，记事件A为“甲获得比赛胜利或者平局”，事件B为“乙获得比赛的胜利或者平局”，已知.

    (1)求甲获得比赛胜利的概率；

    (2)求甲、乙两人获得平局的概率.

    【答案】（1）0.6；(2)0.1.

    【解析】

    由题意，甲、乙两人进行围棋比赛，所有的可能基本事件有：甲获得胜利、乙获得胜利、甲乙平局，它们互为互斥事件，根据互斥事件的概率公式解答。

    甲、乙两人进行围棋比赛，所有的可能基本事件有：甲获得胜利、乙获得胜利、甲乙平局，分别记做事件 、、，且 、、为互斥，则“甲获得比赛胜利或者平局”为事件 、的和事件，“乙获得比赛的胜利或者平局”为、的和事件，由互斥事件的和事件概率公式得：

    又

    ，，

    故甲获得比赛胜利的概率为；

    甲、乙两人获得平局的概率为；

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】为了解春季昼夜温差大小与某种子发芽数之间的关系，现在从4月份的30天中随机挑选了5天进行研究，且分别记录了明天昼夜温差与每天100颗种子浸泡后的发芽数，得到如下表格：

    日期

    4月1日

    4月7日

    4月15日

    4月21日

    4月30日

    温差x/℃

    10

    11

    13

    12

    8

    发芽数y/颗

    23

    25

    30

    26

    16

    从这5天中任选2天，记发芽的种子数分别为，求事件“君不小于25”的概率；

    （2）从这5天中任选2天，若选取的是4月1日与4月30日的两组数据，请根据这5填中的另三天的数据，求出关于的线性回归方程，.

    （参考公式：，）.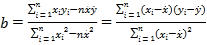

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（本小题满分12分）已知点为抛物线的焦点，点在抛物线上，且．

    （Ⅰ）求抛物线的方程；

    （Ⅱ）已知点，延长交抛物线于点，证明：以点为圆心且与直线相切的圆，必与直线相切．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】三棱柱中，平面平面，，点为棱的中点，点为线段上的动点.

    （1）求证：；

    （2）若直线与平面所成角为，求二面角的正切值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）若函数的图象在点处的切线方程为，求实数a，b的值；

    （2）若，求的单调减区间；

    （3）对一切实数，求的极小值函数，并求出的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某校要从甲、乙两名同学中选择一人参加该市组织的数学竞赛，已知甲、乙两名同学最近7次模拟竞赛的数学成绩（满分100分）如下:

    甲:79，81，83，84，85，90，93；

    乙：75，78，82，84，90，92，94.

    （1）完成答题卡中的茎叶图；

    （2）分别计算甲、乙两名同学最近7次模拟竞赛成绩的平均数与方差，并由此判断该校应选择哪位同学参加该市组织的数学竞赛.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知10件不同产品中有3件是次品，现对它们一一取出（不放回）进行检测，直至取出所有次品为止．

    （1）若恰在第5次取到第一件次品，第10次才取到最后一件次品，则这样的不同测试方法数有多少？

    （2）若恰在第6次取到最后一件次品，则这样的不同测试方法数是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】网络看病就是国内或者国外的单个人、多个人或者单位通过国际互联网或者其他局域网对自我、他人或者某种生物的生理疾病或者机器故障进行查找询问、诊断治疗、检查修复的一种新兴的看病方式.因此，实地看病与网络看病便成为现在人们的两种看病方式，最近某信息机构调研了患者对网络看病，实地看病的满意程度，在每种看病方式的患者中各随机抽取15名，将他们分成两组，每组15人，分别对网络看病，实地看病两种方式进行满意度测评，根据患者的评分（满分100分）绘制了如图所示的茎叶图：

    （1）根据茎叶图判断患者对于网络看病、实地看病那种方式的满意度更高？并说明理由；

    （2）若将大于等于80分视为“满意”，根据茎叶图填写下面的列联表：

    满意

    不满意

    总计

    网络看病

    实地看病

    总计

    并根据列联表判断能否有的把握认为患者看病满意度与看病方式有关？

    （3）从网络看病的评价“满意”的人中随机抽取2人，求这2人平分都低于90分的概率.

    附，其中.

    0.15

    0.10

    0.05

    0.025

    0.010

    0.005

    0.001

    2.072

    2.706

    3.841

    5.024

    6.635

    7.879

    10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】解关于的不等式．

    查看答案和解析>>

    同步练习册答案