
【题目】已知函数f(x)=|4x﹣a|+|4x+3|,g(x)=|x﹣1|﹣|2x|.
(1)解不等式g(x)>﹣3;
(2)若存在x1∈R,也存在x2∈R,使得f(x1)=g(x2)成立,求实数a的取值范围.
【答案】
(1)
解:由题意可得 
因为g(x)>﹣3,
由函数图象可得不等式的解为﹣4<x<2,
所以不等式的解集为{x|﹣4<x<2}
(2)
解:因为存在x1∈R,存在x2∈R,使得f(x1)=g(x2)成立,
所以{y|y=f(x),x∈R}∩{y|y=g(x),x∈R}≠,
又f(x)=|4x﹣a|+|4x+3|≥|(4x﹣a)+(4x+3)|=|a+3|,
由(1)可知g(x)max=1,所以|a+3|≤1,解得﹣4≤a≤﹣2,
所以实数a的取值范围为[﹣4,﹣2].

【解析】(1)通过讨论x的范围求出各个区间上的不等式的解集,取并集即可;(2)因为存在x1∈R,存在x2∈R,使得f(x1)=g(x2)成立,所以{y|y=f(x),x∈R}∩{y|y=g(x),x∈R}≠,分别求出f(x),g(x)的范围,即可求实数a的取值范围.
【考点精析】利用绝对值不等式的解法对题目进行判断即可得到答案,需要熟知含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号.


科目:高中数学 来源: 题型:
【题目】某险种的基本保费为![]() (单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:
(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:
上年度出险次数 | 0 | 1 | 2 | 3 | 4 |
|
保费 |
|
|
|
|
|
|
设该险种一续保人一年内出险次数与相应概率如下:
一年内出险次数 | 0 | 1 | 2 | 3 | 4 |
|
概率 | 0.30 | 0.15 | 0.20 | 0.20 | 0.10 | 0.05 |
(1)求一续保人本年度的保费高于基本保费的概率;
(2)已知一续保人本年度的保费高于基本保费,求其保费比基本保费高出![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx+mx(m为常数).
(1)讨论函数f(x)的单调区间;
(2)当 ![]() 时,设
时,设 ![]() 的两个极值点x1 , x2(x1<x2)恰为h(x)=2lnx﹣ax﹣x2的零点,求
的两个极值点x1 , x2(x1<x2)恰为h(x)=2lnx﹣ax﹣x2的零点,求 ![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校200名学生的数学期中考试成绩频率分布直方图如图所示,其中成绩分组区间是![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
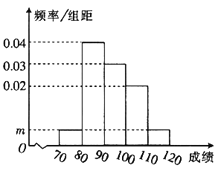
(1)求图中![]() 的值;
的值;
(2)根据频率分布直方图,估计这200名学生的平均分;
(3)若这200名学生的数学成绩中,某些分数段的人数![]() 与英语成绩相应分数段的人数
与英语成绩相应分数段的人数![]() 之比如下表所示,求英语成绩在
之比如下表所示,求英语成绩在![]() 的人数.
的人数.
分数段 |
|
|
|
|
|
| 1:2 | 2:1 | 6:5 | 1:2 | 1:1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了参加某运动会,从四支较强的排球队中选出18人组成女子排球国家队,队员来源人数如下表:
队别 | 北京 | 上海 | 天津 | 八一 |
人数 | 4 | 6 | 3 | 5 |
(1)从这18名队员中随机选出两名,求两人来自同一队的概率;
(2)若要求选出两名队员担任正副队长,设其中来自北京队的人数为![]() ,求随机变量
,求随机变量![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长为2的正方体ABCD﹣A1B1C1D1中,P为棱C1D1的中点,Q为棱BB1上的点,且BQ=λBB1(λ≠0). 
(1)若 ![]() ,求AP与AQ所成角的余弦值;
,求AP与AQ所成角的余弦值;
(2)若直线AA1与平面APQ所成的角为45°,求实数λ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,球![]() 的表面积为
的表面积为![]() ,球心
,球心![]() 为空间直角坐标系
为空间直角坐标系![]() 的原点,且球
的原点,且球![]() 分别与
分别与![]() 轴的正交半轴交于
轴的正交半轴交于![]() 三点,已知球面上一点
三点,已知球面上一点![]() .
.
(1)求![]() 两点在球
两点在球![]() 上的球面距离;
上的球面距离;
(2)过点![]() 作平面
作平面![]() 的垂线,垂足
的垂线,垂足![]() ,求
,求![]() 的坐标,并计算四面体
的坐标,并计算四面体![]() 的体积;
的体积;
(3)求平面![]() 与平面
与平面![]() 所成锐二面角的大小.
所成锐二面角的大小.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com