【题目】在平面直角坐标系中，以坐标原点为极点，x轴的非负半轴为极轴建立极坐标系，已知曲线C的极坐标方程为
，它在点
处的切线为直线l.
(1)求直线l的直角坐标方程；
(2)设直线l与
的交点为P1,P2,求过线段P1P2的中点且与l垂直的直线的极坐标方程.
科目：高中数学 来源： 题型：
【题目】若函数f（x）同时满足以下三个性质；①f（x）的最小正周期为π；②对任意的x∈R，都有f（x﹣ 
）=f（﹣x）；③f（x）在（ 
， 
）上是减函数．则f（x）的解析式可能是（ ）
A.f（x）=cos（x+ 
）
B.f（x）=sin2x﹣cos2x
C.f（x）=sinxcosx
D.f（x）=sin2x+cos2x
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，已知三棱锥P﹣ABC，PA⊥平面ABC，∠ACB=90°，∠BAC=60°，PA=AC，M为PB的中点． 
（Ⅰ）求证：PC⊥BC．
（Ⅱ）求二面角M﹣AC﹣B的大小．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，已知椭圆
（
）的离心率为
，以该椭圆上的点和椭圆的左、右焦点
，
为顶点的三角形的周长为
，一等轴双曲线的顶点是该椭圆的焦点，设
为该双曲线上异于顶点的任一点，直线
和
与椭圆的交点分别为
、
和
、
．
（1）求椭圆和双曲线的标准方程；
（2）设直线、的斜率分别为
、
，证明
为定值；
（3）是否存在常数
，使得
恒成立？若存在，求的值；若不存在，请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在多面体ABCDEF中，四边形ABCD为边长为4的正方形，M是BC的中点，EF∥平面ABCD，且EF=2，AE=DE=BF=CF= 
． 
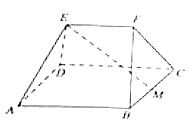
（1）求证：ME⊥平面ADE；
（2）求二面角B﹣AE﹣D的余弦值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】随着南宁三中集团化发展，南宁三中青三校区2018年被清华北大录取23人，广西领先，一本率连年攀升，南宁三中青山校区2014年至2018年一本率如下表：
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
时间代号 | 1 | 2 | 3 | 4 | 5 |
一本率 | 0.7152 | 0.7605 | 0.7760 | 0.8517 | 0.9015 |
(1)求
关于
的回归方程
(精确到0.0001);
(2)用所求回归方程预测南宁三中青山校区2019年高考一本录取率.(精确到0.0001).
附：回归方程中
参考数据：
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】右图是一个几何体的平面展开图，其中ABCD为
正方形， E、F分别为PA、PD的中点，在此几何体中，
给出下面四个结论：
①直线BE与直线CF异面；②直线BE与直线AF异面；
③直线EF//平面PBC； ④平面BCE⊥平面PAD.
其中正确结论的个数是
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，三角形ABC和梯形ACEF所在的平面互相垂直，AB⊥BC，AF⊥AC，AF 
2CE，G是线段BF上一点，AB=AF=BC． 
（Ⅰ）若EG∥平面ABC，求 
的值；
（Ⅱ）求二面角A﹣BF﹣E的大小的正弦值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
