
【题目】如图,四面体ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD.

(1)证明:平面ACD⊥平面ABC;
(2)过AC的平面交BD于点E,若平面AEC把四面体ABCD分成体积相等的两部分,求二面角D–AE–C的余弦值.
【答案】(1)证明见解析;
(2) ![]() .
.
【解析】
(1)利用题意,证得二面角为![]() ,即可得到平面ACD⊥平面ABC;
,即可得到平面ACD⊥平面ABC;
(2)建立适当的空间直角坐标系,求得两个半平面的法向量,利用向量的夹角公式,即可求解二面角的余弦值。
(1)由题意可得,![]() ,从而
,从而![]() ,
,
又![]() 是直角三角形,所以
是直角三角形,所以![]() ,
,
取AC的中点O,连接DO,BO,则![]() ,
,
又由![]() 是正三角形,所以
是正三角形,所以![]() ,
,
所以![]() 是二面角
是二面角![]() 的平面角,
的平面角,
在直角![]() 中,
中,![]() ,
,
又,![]() 所以
所以![]() ,故
,故![]() ,
,
所以平面![]() 平面
平面![]() 。
。
(2)由题设及(1)可知![]() ,
,![]() ,
,![]() 两两垂直,以
两两垂直,以![]() 为坐标原点,建立如图所示的空间直角坐标系
为坐标原点,建立如图所示的空间直角坐标系![]() ,
,
则![]()
由题设知,四面体![]() 的体积为四面体
的体积为四面体![]() 的体积的
的体积的![]() ,从而
,从而![]() 到平面
到平面![]() 的距离为
的距离为![]() 到平面
到平面![]() 的距离的
的距离的![]() ,即
,即![]() 为
为![]() 的中点,得
的中点,得![]() .
.
故![]() ,
,
设![]() 是平面
是平面![]() 的法向量,则
的法向量,则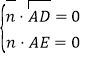 ,即
,即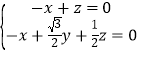 ,
,
令![]() ,则
,则![]() ,即平面
,即平面![]() 的一个法向量
的一个法向量![]() ,
,
设![]() 是平面
是平面![]() 的法向量,则
的法向量,则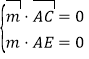 ,
,
可得平面![]() 的一个法向量
的一个法向量![]() ,
,
则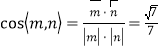 ,即二面角
,即二面角![]() 的余弦值为
的余弦值为![]() 。
。


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】为调查某小区居民的“幸福度”。现从所有居民中随机抽取16名,如图所示的茎叶图记录了他们的幸福度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶),若幸福度分数不低于8.5分,则称该人的幸福度为“幸福”。

(1)求从这16人中随机选取3人,至少有2人为“幸福”的概率;
(2)以这16人的样本数据来估计整个小区的总体数据,若从该小区(人数很多)任选3人,记![]() 表示抽到“幸福”的人数,求
表示抽到“幸福”的人数,求![]() 的分布列及数学期望和方差。
的分布列及数学期望和方差。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】f(x)是定义在(0,+∞)上的单调增函数,满足f(xy)=f(x)+f(y),f(3)=1,当f(x)+f(x-8)≤2时,x的取值范围是( )
A.(8,+∞)B.(8,9]C.[8,9]D.(0,8)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“每天锻炼一小时,健康工作五十年,幸福生活一辈子.”一科研单位为了解员工爱好运动是否与性别有关,从单位随机抽取30名员工进行了问卷调查,得到了如下列联表:
男性 | 女性 | 合计 | |
爱好 | 10 | ||
不爱好 | 8 | ||
合计 | 30 |
已知在这30人中随机抽取1人抽到爱好运动的员工的概率是![]() .
.
(1)请将上面的列联表补充完整(在答题卷上直接填写结果,不需要写求解过程),并据此资料分析能否有把握认为爱好运动与性别有关?
(2)若从这30人中的女性员工中随机抽取2人参加一活动,记爱好运动的人数为![]() ,求
,求![]() 的分布列、数学期望.参考数据:
的分布列、数学期望.参考数据:
| 0.10 | 0.05 | 0.025 | 0.01 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024/span> | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是函数
是函数![]() 定义域的一个子集,若存在
定义域的一个子集,若存在![]() ,使得
,使得![]() 成立,则称
成立,则称![]() 是
是![]() 的一个“准不动点”,也称
的一个“准不动点”,也称![]() 在区间
在区间![]() 上存在准不动点,已知
上存在准不动点,已知![]() ,
,![]() .
.
(1)若![]() ,求函数
,求函数![]() 的准不动点;
的准不动点;
(2)若函数![]() 在区间
在区间![]() 上存在准不动点,求实数
上存在准不动点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,若函数
,若函数![]() 有三个不同的零点
有三个不同的零点![]() ,
,![]() ,
,![]() (其中
(其中![]() ),则
),则![]() 的取值范围为__________.
的取值范围为__________.
【答案】![]()
【解析】如图:

![]() ,
,![]() ,作出函数图象如图所示
,作出函数图象如图所示
![]() ,
,![]() ,作出函数图象如图所示
,作出函数图象如图所示
![]()
![]() ,由
,由![]() 有三个不同的零点
有三个不同的零点
![]() ,如图
,如图
令![]()
![]()
得![]()
![]()
为满足有三个零点,如图可得
![]() ,
,![]()
![]()
![]()
点睛:本题考查了函数零点问题,先由导数求出两个函数的单调性,继而画出函数图像,再由函数的零点个数确定参量取值范围,将问题转化为函数的两根问题来求解,本题需要化归转化,函数的思想,零点问题等较为综合,有很大难度。
【题型】填空题
【结束】
17
【题目】已知等比数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)若数列![]() 满足
满足![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了估计某校某次数学考试的情况,现从该校参加考试的600名学生中随机抽出60名学生,其数学成绩(百分制)均在![]() 内,将这些成绩分成六组
内,将这些成绩分成六组![]() …
…![]() ,得到如图所示的部分频率分布直方图.
,得到如图所示的部分频率分布直方图.

(1)求抽出的60名学生中数学成绩在![]() 内的人数;
内的人数;
(2)若规定成绩不小于85分为优秀,则根据频率分布直方图,估计该校参加考试的学生数学成绩为优秀的人数;
(3)试估计抽出的60名学生的数学成绩的中位数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com