
| A. | (-18,-16) | B. | [-18,-16] | C. | (-22,-18) | D. | (-20,-18) |
分析 数列{an}的前项和为Sn=n(2n+a),由此能求出{an}的通项公式an=4n-2+a,得到数列为等差数列,根据求和公式得到Sn=2n2+an,求出S5=50+5a,由前n项和Sn≥S5恒成立,得到a(5-n)≤2(n+5)(n-5),分类讨论,即可求出a的范围.
解答 解:∵数列{an}的前n项的“均倒数”为$\frac{1}{2n+a}$,
∴根据题意得数列{an}的前项和为:Sn=n(2n+a),
当n≥2时,an=Sn-Sn-1=n(2n+a)-(n-1)(2n-2+a)=4n-2+a,
n=1时,a1=S1=2+a适合上式,
∴an=4n-2+a,
∴an-an-1=4n-2+a-4(n-1)+2-a=4,
∴数列{an}为等差数列,
∴Sn=$\frac{n(2+a+4n-2+a)}{2}$=2n2+an,
∴S5=50+5a,
∵Sn≥S5恒成立,
∴2n2+an≥50+5a,
∴a(5-n)≤2n2-50=2(n+5)(n-5)
当n<5时,a≤-2(n+5),
∵-2(n+5)<-18,
∴a<-18;
当n>5时,a≥-2(n+5),
∵-2(n+5)<-22,
∴a>-22
当n=5时,a取任何数都成立.
综上所述a的取值范围为(-22,-18),
故选:C
点评 本题考查数列的通项公式和前n项和的求法,以及恒成立的问题,是中档题,解题时要认真审题.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:解答题
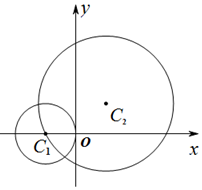 已知圆${C_1}:{x^2}+{y^2}+2x=0$,圆${C_2}:{x^2}+{y^2}-2x-2y-2=0$,C1,C2分别为两圆的圆心.
已知圆${C_1}:{x^2}+{y^2}+2x=0$,圆${C_2}:{x^2}+{y^2}-2x-2y-2=0$,C1,C2分别为两圆的圆心.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | lg101 | B. | 1 | C. | 2 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知函数f(x)=|x-2|-|x+2|.
已知函数f(x)=|x-2|-|x+2|.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $6\sqrt{2}$ | B. | $4\sqrt{5}$ | C. | $2\sqrt{34}$ | D. | 72 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{27\sqrt{3}}{4}$ | B. | $\frac{9\sqrt{3}}{4}$ | C. | $\frac{3\sqrt{3}}{4}$ | D. | $\frac{\sqrt{3}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ①③ | C. | ②④ | D. | ①④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com