
分析 (Ⅰ)计算事件A发生的概率即可;
(Ⅱ)根据题意知X的可能取值为0,1,2,3,4;计算对应的概率值,写出X的分布列与数学期望.
解答 解:(Ⅰ)A为事件“选出的四人中恰有两名女性,且这两名女性不都是预备党员”,
则事件A发生的概率为
P(A)=$\frac{{C}_{2}^{2}{•C}_{4}^{2}{+C}_{2}^{1}{•C}_{2}^{1}{•C}_{4}^{2}}{{C}_{8}^{4}}$=$\frac{3}{7}$;
(Ⅱ)设X为选出的4人中男党员的人数,则X的可能取值为0,1,2,3,4;
且P(X=k)=$\frac{{C}_{4}^{k}{•C}_{4}^{4-k}}{{C}_{8}^{4}}$,(k=0,1,2,3,4)
∴P(X=0)=$\frac{{C}_{4}^{0}{•C}_{4}^{4}}{{C}_{8}^{4}}$=$\frac{1}{70}$,
P(X=1)=$\frac{{C}_{4}^{1}{•C}_{4}^{3}}{{C}_{8}^{4}}$=$\frac{8}{35}$,
P(X=2)=$\frac{{C}_{4}^{2}{•C}_{4}^{2}}{{C}_{8}^{4}}$=$\frac{18}{35}$,
P(X=3)=$\frac{{C}_{4}^{3}{•C}_{4}^{1}}{{C}_{8}^{4}}$=$\frac{8}{35}$,
P(X=4)=$\frac{{C}_{4}^{4}{•C}_{4}^{0}}{{C}_{8}^{4}}$=$\frac{1}{70}$;
∴随机变量X的分布列为:
| X | 0 | 1 | 2 | 3 | 4 |
| P | $\frac{1}{70}$ | $\frac{8}{35}$ | $\frac{18}{35}$ | $\frac{8}{35}$ | $\frac{1}{70}$ |
点评 本题考查了概率的求法以及离散型随机变量的分布列和数学期望的计算问题,是中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数f(x)的图象向左平移$\frac{π}{3}$个单位得到的函数是偶函数 | |
| B. | 不等式f(x1)f(x2)≤4取到等号时|x1-x2|的最小值为2π | |
| C. | 函数f(x)的图象的一个对称中心为($\frac{2}{3}$π,0) | |
| D. | 函数f(x)在区间[$\frac{π}{6}$,π]上单调递增 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
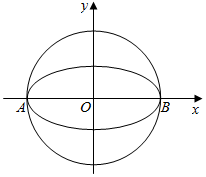 如图,椭圆W:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,其左顶点A在圆O:x2+y2=16上.
如图,椭圆W:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,其左顶点A在圆O:x2+y2=16上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -1 | C. | 5 | D. | 11 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com