
����Ŀ���Ӽ�������������߲��Դ��в���ũҩ��ʳ��ʱ��Ҫ��ϴ���Σ�ͳ�Ʊ��е�![]() ��ʾ��ϴ�Ĵ�����
��ʾ��ϴ�Ĵ�����![]() ��ʾ��ϴ
��ʾ��ϴ![]() �κ�
�κ�![]() ǧ�˸��߲˲�����ũҩ������λ���ˣ���
ǧ�˸��߲˲�����ũҩ������λ���ˣ���
x | 1 | 2 | 3 | 4 | 5 |
y | 4.5 | 2.2 | 1.4 | 1.3 | 0.6 |
��1������ͼ������ϵ�У����ɢ��ͼ��������ɢ��ͼ�жϣ�![]() ��
��![]() ��һ��������Ϊ��ϴ
��һ��������Ϊ��ϴ![]() �κ�
�κ�![]() ǧ�˸��߲˲�����ũҩ���Ļع鷽�����ͣ��������жϼ��ɣ�����˵�����ɣ�
ǧ�˸��߲˲�����ũҩ���Ļع鷽�����ͣ��������жϼ��ɣ�����˵�����ɣ�

��2�������жϼ���������е����ݣ�����![]() ����
����![]() �Ļع鷽�̣�
�Ļع鷽�̣�
����![]() ��
��![]() ��
��
|
|
|
|
|
| |
3 | 2 | 0.12 | 10 | 0.09 | -8.7 | 0.9 |
��3��������Ļع鷽�̽��вв������
���������Իع鷽��![]() ��ϵ�����㹫ʽ�ֱ�Ϊ
��ϵ�����㹫ʽ�ֱ�Ϊ ��
��![]() ��
��
�� ��
��![]() ˵��ģ��Ч���dz��ã�
˵��ģ��Ч���dz��ã�
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
���𰸡���1������������2��![]() ����3�����Ч���dz��ã�
����3�����Ч���dz��ã�
��������
��1���ȸ�����������ɢ��ͼ�����ɢ��ͼ�����жϣ�
��2������![]() ��
��![]() ������ع�ʽ����
������ع�ʽ����![]() ����
����![]() �Ļع鷽�̣�
�Ļع鷽�̣�
��3����������ֵ����ʵ���ݼ�IJ���ݹ�ʽ���![]() ��Ȼ������ж�.
��Ȼ������ж�.
��1��ɢ��ͼ��ͼ��
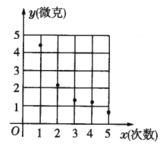
����ɢ��ͼ��֪��![]() ��Ϊ��ϴ
��Ϊ��ϴ![]() �κ�
�κ�![]() ǧ�˸��߲˲�����ũҩ���Ļع鷽�����ͣ�
ǧ�˸��߲˲�����ũҩ���Ļع鷽�����ͣ�
��2������֪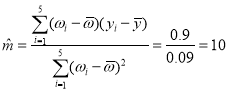 ��
��![]() ��
��
������Ļع鷽��Ϊ![]() ��
��
��3���б����£�
| 0 | 0 | 0.1 | 0.3 | -0.3 |
| 2.5 | 0.2 | -0.6 | -0.7 | -1.4 |
����![]() ��
��![]() ��
��![]() ��
��
���Իع�ģ������Ч���dz��ã�


 �ܿ�����ĩ��̾�ϵ�д�
�ܿ�����ĩ��̾�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������x�IJ���ʽ2lnx��ax2+��2a��2��x+1���������a����С����ֵ�ǣ� ��
A.0B.1C.2D.3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������![]() ��������
��������![]() ��
��![]() ����
����![]() ����
����![]() ���趯��
���趯��![]() �Ĺ켣Ϊ
�Ĺ켣Ϊ![]() ��
��
��1����켣![]() �ķ��̣�
�ķ��̣�
��2����ֱ��![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ����켣
����켣![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ����
����![]() ����
����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��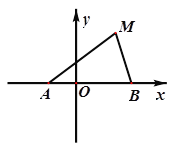
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ں���![]() �������ĸ����ۣ�
�������ĸ����ۣ�
��![]() ��ż��������
��ż��������![]() �����ֵΪ
�����ֵΪ![]() ��
��
��![]() ��
��![]() ��
��![]() ����㣻��
����㣻��![]() ������
������![]() ��������.
��������.
����������ȷ���۵ı���ǣ� ��
A.�٢�B.�٢�C.�ڢ�D.�٢�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ����ij��˾�������������������ù�˾����ռ���һ�������۵��й����ݣ���˾�涨ͬһ��������ۼ۸���ͬ�������������õ��±���
�������� | ��һ�� | �ڶ��� | ������ | ������ | ������ |
�����ܶ��Ԫ�� |
|
|
|
|
|
��������̨�� |
|
|
|
|
|
������ |
|
|
|
|
|
��������ָ��һ̨�������ۼ۸��ȥ�����۸�õ���������û������ۼ۸�ı�ֵ��
���Ӹù�˾���������Ļ��������ѡһ̨������̨���������ʸ���0.2�ĸ��ʣ�
���Ӹù�˾�������������۵���Ϊ20��Ԫ�Ļ��������ѡȡ![]() ̨��������̨�����������ʲ�ͬ�ĸ��ʣ�
̨��������̨�����������ʲ�ͬ�ĸ��ʣ�
������ÿ����������ʲ��䣬����һ̨��һ���������![]() ��Ԫ������һ̨�ڶ����������
��Ԫ������һ̨�ڶ����������![]() ��Ԫ����������һ̨�������������
��Ԫ����������һ̨�������������![]() �������ϱ�ͳ�����ݣ��������һ̨��������������Ϊ
�������ϱ�ͳ�����ݣ��������һ̨��������������Ϊ![]() ����
����![]() �����ж�
�����ж�![]() ��
��![]() �Ĵ�С�������۲�Ҫ��֤����
�Ĵ�С�������۲�Ҫ��֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����˾Ϊ����ʵ����Ա���Ľ�����ȫ���᳹���������߹��������Ҫ������ȫ��˾��Χ�ھ���һ���Ҹ��ղ飬Ϊ����Ҫ����960�˵�Ѫ�����л��飬���������϶࣬���߲����ƶ����������ֿɹ�ѡ��ķ���.
�����٣���ÿ���˵�Ѫ�ֱ��飬��ʱ��Ҫ��960��.
�����ڣ���![]() ����һ�����������飬�Ѵ�ÿ��
����һ�����������飬�Ѵ�ÿ��![]() ���˳�����Ѫ�����һ����м��飬���ÿ���˵�Ѫ��Ϊ���ԣ�������Ľ�������ԣ���
���˳�����Ѫ�����һ����м��飬���ÿ���˵�Ѫ��Ϊ���ԣ�������Ľ�������ԣ���![]() ���˵�Ѫ��ֻ�����һ�Σ������������ԣ��������
���˵�Ѫ��ֻ�����һ�Σ������������ԣ��������![]() ���˵�Ѫ���ٷֱ����һ�λ��飬����������
���˵�Ѫ���ٷֱ����һ�λ��飬����������![]() ���˵�Ѫ�ܹ���Ҫ����
���˵�Ѫ�ܹ���Ҫ����![]() ��.
��.
����˴��ղ���ÿ���˵�Ѫ����������Եĸ���Ϊ![]() ������Щ��֮������鷴Ӧ�����.
������Щ��֮������鷴Ӧ�����.
��1���跽�����У�ij��![]() ������ÿ���˵�Ѫ�������Ϊ
������ÿ���˵�Ѫ�������Ϊ![]() ����
����![]() �ķֲ��У�
�ķֲ��У�
��2����![]() ���ԱȽϷ������У�
���ԱȽϷ������У�![]() �ֱ�ȡ2��3��4ʱ�����軯���ƽ���ܴ�������ָ���������ַ�������£���ȷ����٣��������������ƽ�����ٶ��ٴΣ�(������������뱣������).
�ֱ�ȡ2��3��4ʱ�����軯���ƽ���ܴ�������ָ���������ַ�������£���ȷ����٣��������������ƽ�����ٶ��ٴΣ�(������������뱣������).
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1���ԱȽ�![]() ��
��![]() �Ĵ�С.
�Ĵ�С.
��2��������![]() ���������ֱ�Ϊ
���������ֱ�Ϊ![]() ��
��![]() ��
��
����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��֤����![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��λ��2019����������֯50������ְ�����С�Ů��25��������,����ְ������ѡ�ס���������������һ��ȥ����.��������ѡ��ľ���Ľ�����±���
���� | �� | |
���� | 20 | 10 |
�Ҿ��� | 5 | 15 |
��1���ݴ����Ϸ���,�Ƿ���![]() �İ�����Ϊѡ���ĸ��������Ա��йأ�
�İ�����Ϊѡ���ĸ��������Ա��йأ�
��2������������ͬ�����÷ֲ�����ķ���,��Ůְ����ѡȡ5��,�ٴ���5���������ȡ2�˽��вɷ�,����2�������ľ��㲻ͬ�ĸ���.
����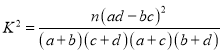 ,
,![]() .
.
P�� | 0.010 | 0.005 | 0.001 |
k | 6.635 | 7.879 | 10.828 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������![]() �У�
�У�![]() ƽ��
ƽ��![]() ��
��![]() ƽ��
ƽ��![]() ��
��![]() ��
��![]() ��
��![]() Ϊ
Ϊ![]() ���е㣮
���е㣮
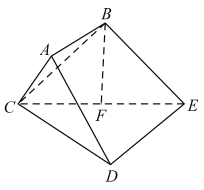
��1����֤��![]() ƽ��
ƽ��![]() ��
��
��2���������![]() �������
�������
��3����ƽ��![]() ��ƽ��
��ƽ��![]() ���ɵ������ǵĴ�С��
���ɵ������ǵĴ�С��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com