
分析 直接利用三角函数的化简求值判断①;利用换元法求出函数sinx+cosx+sinxcosx最大值判断②;利用数形结合求出y=$\frac{sinx+1}{cosx+2}$的最大值判断③;利用换元法求出函数y=x+$\sqrt{4-{x^2}}$的最大值判断④.
解答 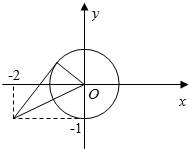 解:①4cos10°-tan80°=4cos10°-$\frac{sin80°}{cos10°}$=4cos10°-$\frac{cos10°}{sin10°}$
解:①4cos10°-tan80°=4cos10°-$\frac{sin80°}{cos10°}$=4cos10°-$\frac{cos10°}{sin10°}$
=$\frac{4sin10°cos10°-cos10°}{sin10°}$=$\frac{2sin20°-cos10°}{sin10°}$=$\frac{2sin20°-cos(30°-20°)}{sin10°}$
=$\frac{\frac{3}{2}sin20°-\frac{\sqrt{3}}{2}cos20°}{sin10°}$=$\frac{\sqrt{3}(\frac{\sqrt{3}}{2}sin20°-\frac{1}{2}cos20°)}{sin10°}$=$\frac{\sqrt{3}sin(-10°)}{sin10°}=-\sqrt{3}$,①错误;
②令sinx+cosx=t($-\sqrt{2}≤t≤\sqrt{2}$),
由同角三角函数关系得sinxcosx=$\frac{{t}^{2}-1}{2}$,
∴y=$t+\frac{{t}^{2}-1}{2}=\frac{{t}^{2}}{2}+t-\frac{1}{2}$,当t=-1时,y取得最小值=-1,当T=$\sqrt{2}$时,y取得最大值$\sqrt{2}+\frac{1}{2}$,②错误;
③y=$\frac{sinx+1}{cosx+2}$的几何意义为圆x2+y2=1上的动点与定点(-2,-1)连线的斜率,如图,
最大值k=$\frac{2×\frac{1}{2}}{1-(\frac{1}{2})^{2}}=\frac{4}{3}$,③错误;
④由y=x+$\sqrt{4-{x^2}}$,令x=2sinα($-\frac{π}{2}≤α≤\frac{π}{2}$),则4-x2=4-4sin2α=4cos2α,
∴y=2sinα+2cosα=$2\sqrt{2}sin(α+\frac{π}{4})$∈[-2,2$\sqrt{2}$],④正确.
故答案为:④.
点评 本题考查命题的真假判断与应用,考查了三角函数的化简与求值,训练了三角函数最值的求法,是中档题.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
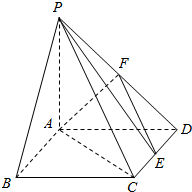 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,且PA=AD,点F是棱PD的中点,点E在棱CD上移动.求证:PE⊥AF.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,且PA=AD,点F是棱PD的中点,点E在棱CD上移动.求证:PE⊥AF.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 关于直线x=$\frac{π}{6}$对称 | B. | 关于直线x=$\frac{π}{4}$对称. | ||
| C. | 关于点($\frac{π}{4}$,0)对称 | D. | 关于点($\frac{π}{6}$,0)对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com