
【题目】已知函数f(x)=( ![]() )x , 其反函数为y=g(x).
)x , 其反函数为y=g(x).
(1)若g(mx2+2x+1)的定义域为R,求实数m的取值范围;
(2)当x∈[﹣1,1]时,求函数y=[f(x)]2﹣2af(x)+3的最小值h(a);
(3)是否存在实数m>n>3,使得函数y=h(x)的定义域为[n,m],值域为[n2 , m2],若存在,求出m、n的值;若不存在,则说明理由.
【答案】
(1)解:∵函数f(x)=( ![]() )x,则其反函数为y=g(x)=
)x,则其反函数为y=g(x)= ![]() =﹣log3x.
=﹣log3x.
∴g(mx2+2x+1)=﹣ ![]() ,
,
当m≤0时,g(mx2+2x+1)的定义域不为R,舍去.
当m>0时,g(mx2+2x+1)的定义域为R,则 ![]() ,解得m>1.
,解得m>1.
∴实数m的取值范围是(1,+∞)
(2)解:函数y=[f(x)]2﹣2af(x)+3= ![]() ﹣2a
﹣2a ![]() +3,
+3,
∵x∈[﹣1,1]时,令 ![]() =t∈
=t∈ ![]() ,
,
∴y=t2﹣2at+3=(t﹣a)2+3﹣a2=u(t),对称轴t=a.
当a ![]() 时,u(t)在t∈
时,u(t)在t∈ ![]() 上单调递增,∴t=
上单调递增,∴t= ![]() 时,u(t)取得最小值u(
时,u(t)取得最小值u( ![]() )=
)= ![]() .
.
当a≥3时,u(t)在t∈ ![]() 上单调递减,∴t=3时,u(t)取得最小值u(3)=12﹣6a.
上单调递减,∴t=3时,u(t)取得最小值u(3)=12﹣6a.
当 ![]() <a<3时,u(t)在t∈
<a<3时,u(t)在t∈ ![]() 上单调递减,在t∈[a,3]上单调递增,∴t=a时,u(t)取得最小值u(a)=3﹣a2.
上单调递减,在t∈[a,3]上单调递增,∴t=a时,u(t)取得最小值u(a)=3﹣a2.
综上可得:最小值h(a)= 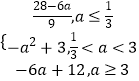
(3)解:存在实数m>n>3,使得函数y=h(x)=﹣6x+12的定义域为[n,m],值域为[n2,m2],
则 ![]() ,可得:m2﹣6m+24=0,由于△=36﹣96<0,因此上述方程无解.
,可得:m2﹣6m+24=0,由于△=36﹣96<0,因此上述方程无解.
于是假设不成立,
因此不存在实数m>n>3,使得函数y=h(x)=﹣6x+12的定义域为[n,m],值域为[n2,m2].
【解析】(1)函数f(x)=( ![]() )x , 则其反函数为y=g(x)=
)x , 则其反函数为y=g(x)= ![]() .可得g(mx2+2x+1)=﹣
.可得g(mx2+2x+1)=﹣ ![]() ,当m≤0时,舍去.当m>0时,g(mx2+2x+1)的定义域为R,可得
,当m≤0时,舍去.当m>0时,g(mx2+2x+1)的定义域为R,可得 ![]() ,解得m即可得出.(2)函数y=[f(x)]2﹣2af(x)+3=
,解得m即可得出.(2)函数y=[f(x)]2﹣2af(x)+3= ![]() ﹣2a
﹣2a ![]() +3,x∈[﹣1,1]时,令
+3,x∈[﹣1,1]时,令 ![]() =t∈
=t∈ ![]() ,y=(t﹣a)2+3﹣a2=u(t),对称轴t=a.对a与
,y=(t﹣a)2+3﹣a2=u(t),对称轴t=a.对a与 ![]() ,3的大小分类讨论,利用二次函数的单调性即可得出.(3)存在实数m>n>3,使得函数y=h(x)=﹣6x+12的定义域为[n,m],值域为[n2 , m2],可得
,3的大小分类讨论,利用二次函数的单调性即可得出.(3)存在实数m>n>3,使得函数y=h(x)=﹣6x+12的定义域为[n,m],值域为[n2 , m2],可得 ![]() ,解出即可判断出结论.
,解出即可判断出结论.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)为对数函数,并且它的图象经过点(2 ![]() ,
, ![]() ),g(x)=[f(x)]2﹣2bf(x)+3,其中b∈R.
),g(x)=[f(x)]2﹣2bf(x)+3,其中b∈R.
(1)求函数f(x)的解析式;
(2)求函数y=g(x)在区间[ ![]() ,16]上的最小值.
,16]上的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产一种电子仪器的固定成本为20000元,每生产一台仪器需增加投入100元,已知总收益满足函数:R(x)=  ,其中x是仪器的月产量.(注:总收益=总成本+利润)
,其中x是仪器的月产量.(注:总收益=总成本+利润)
(1)将利润x表示为月产量x的函数;
(2)当月产量为何值时,公司所获利润最大?最大利润为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,函数g(x)=b﹣f(2﹣x),其中b∈R,若函数y=f(x)﹣g(x)恰有4个零点,则b的取值范围是( )
,函数g(x)=b﹣f(2﹣x),其中b∈R,若函数y=f(x)﹣g(x)恰有4个零点,则b的取值范围是( )
A.( ![]() ,+∞)
,+∞)
B.(﹣∞, ![]() )
)
C.(0, ![]() )
)
D.( ![]() ,2)
,2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“杨辉三角”又称“贾宪三角”,是因为贾宪约在公元1050年首先使用“贾宪三角”进行高次开方运算,而杨辉在公元1261年所著的《详解九章算法》一书中,记录了贾宪三角形数表,并称之为“开方作法本源”图.下列数表的构造思路就源于“杨辉三角”.该表由若干行数字组成,从第二行起,每一行中的数字均等于其“肩上”两数之和,表中最后一行仅有一个数,则这个数是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“杨辉三角”又称“贾宪三角”,是因为贾宪约在公元1050年首先使用“贾宪三角”进行高次开方运算,而杨辉在公元1261年所著的《详解九章算法》一书中,记录了贾宪三角形数表,并称之为“开方作法本源”图.下列数表的构造思路就源于“杨辉三角”.该表由若干行数字组成,从第二行起,每一行中的数字均等于其“肩上”两数之和,表中最后一行仅有一个数,则这个数是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】六个面都是平行四边形的四棱柱称为平行六面体.已知在平行四边形ABCD中(如图1),有AC2+BD2=2(AB2+AD2),则在平行六面体ABCD﹣A1B1C1D1中(如图2),AC12+BD12+CA12+DB12等于( ) 
A.2(AB2+AD2+AA12)
B.3(AB2+AD2+AA12)
C.4(AB2+AD2+AA12)
D.4(AB2+AD2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com