设{an}是各项为正数的无穷数列,Ai是边长为ai,ai+1的矩形的面积(i=1,2,…),则{An}为等比数列的充要条件是( )
A.{an}是等比数列
B.a1,a3,…,a2n-1,…或a2,a4,…,a2n,…是等比数列
C.a1,a3,…,a2n-1,…和a2,a4,…,a2n,…均是等比数列
D.a1,a3,…,a2n-1,…和a2,a4,…,a2n,…均是等比数列,且公比相同
【答案】
分析:根据题意可表示A
i,先看必要性,{A
n}为等比数列推断出
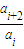
为常数,可推断出a
1,a
3,…,a
2n-1,…和a
2,a
4,…,a
2n,…均是等比数列,且公比相同;再看充分性,要使题设成立,需要

为常数,即a
1,a
3,…,a
2n-1,…和a
2,a
4,…,a
2n,…均是等比数列,且公比相等,答案可得.
解答:解:依题意可知A
i=a
i•a
i+1,
∴A
i+1=a
i+1•a
i+2,
若{A
n}为等比数列则

=

=q(q为常数),则a
1,a
3,…,a
2n-1,…和a
2,a
4,…,a
2n,…均是等比数列,且公比均为q;
反之要想{A
n}为等比数列则

=

需为常数,即需要a
1,a
3,…,a
2n-1,…和a
2,a
4,…,a
2n,…均是等比数列,且公比相等;
故{A
n}为等比数列的充要条件是a
1,a
3,…,a
2n-1,…和a
2,a
4,…,a
2n,…均是等比数列,且公比相同.
故选D
点评:本题主要考查了等比数列的性质,充分条件,必要条件和充分必要条件的判定.考查了学生分析问题和基本的推理能力.

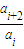 为常数,可推断出a1,a3,…,a2n-1,…和a2,a4,…,a2n,…均是等比数列,且公比相同;再看充分性,要使题设成立,需要
为常数,可推断出a1,a3,…,a2n-1,…和a2,a4,…,a2n,…均是等比数列,且公比相同;再看充分性,要使题设成立,需要 为常数,即a1,a3,…,a2n-1,…和a2,a4,…,a2n,…均是等比数列,且公比相等,答案可得.
为常数,即a1,a3,…,a2n-1,…和a2,a4,…,a2n,…均是等比数列,且公比相等,答案可得. =
= =q(q为常数),则a1,a3,…,a2n-1,…和a2,a4,…,a2n,…均是等比数列,且公比均为q;
=q(q为常数),则a1,a3,…,a2n-1,…和a2,a4,…,a2n,…均是等比数列,且公比均为q; =
= 需为常数,即需要a1,a3,…,a2n-1,…和a2,a4,…,a2n,…均是等比数列,且公比相等;
需为常数,即需要a1,a3,…,a2n-1,…和a2,a4,…,a2n,…均是等比数列,且公比相等;

 在xoy平面上有一系列点P1(x1,y1),P2(x2,y2),…,Pn(xn,yn),…,对每个正整数n,以点Pn为圆心的⊙Pn与x轴及射线y=
在xoy平面上有一系列点P1(x1,y1),P2(x2,y2),…,Pn(xn,yn),…,对每个正整数n,以点Pn为圆心的⊙Pn与x轴及射线y=