
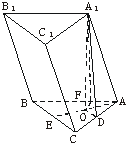
| 解:由题意可知,这个斜三棱柱可以看作是将正三棱柱沿着侧棱AA1正对着侧面BCC1B1的方向推斜而成的,要求它的全面积,关键在于求侧面C1B1BC的面积,根据直觉可以推断侧面C1B1BC是矩形,因此应该先来证明侧面C1B1BC是矩形.
作A1O⊥底面ABC于O,在底面上过O作OD⊥AC于点D,作OF⊥AB于点F,连结A1D、A1F,由AB⊥OF、AB⊥A1O,可得AB⊥面A1FO,∴AB⊥A1F.同理AC⊥A1D. 易证Rt△A1AD≌Rt△A1AF. ∴A1D=AD=AF= ∴Rt△FAO≌Rt△DAO.因此∠BAO=∠CAO=30°,∴OD= 设AO的延长线交BC于点E,则BC⊥AE. 又∵BC⊥A1O,∴BC⊥面A1AO.∴BC⊥A1A. 又∵A1A∥B1B,∴BC⊥B1B,即侧面C1B1BC是矩形. 在Rt△A1AO中,可得A1O= ∴S全=2×2×
|


科目:高中数学 来源: 题型:
 已知斜三棱柱ABC-A1B1C1,∠BCA=90°,AC=BC=2,A1在底面ABC上的射影恰为AC的中点D,又知BA1⊥AC1.
已知斜三棱柱ABC-A1B1C1,∠BCA=90°,AC=BC=2,A1在底面ABC上的射影恰为AC的中点D,又知BA1⊥AC1.查看答案和解析>>
科目:高中数学 来源: 题型:
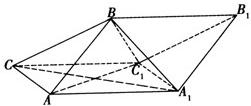 如图,斜三棱柱ABC-A1B1C1的侧面AA1C1C是面积为
如图,斜三棱柱ABC-A1B1C1的侧面AA1C1C是面积为
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知斜三棱柱ABC-A1B1C1,∠BCA=90°,AC=BC=2,A1在底面ABC上的射影恰为AC的中点D,且BA1⊥AC1.
如图,已知斜三棱柱ABC-A1B1C1,∠BCA=90°,AC=BC=2,A1在底面ABC上的射影恰为AC的中点D,且BA1⊥AC1.查看答案和解析>>
科目:高中数学 来源: 题型:
 (2010•抚州模拟)在斜三棱柱ABC-A1B1C1中,AB=BC=2,∠ABC=120°,又顶点A1在底面ABC上的射影落在AC上,侧棱AA1与底面ABC成60°角,D为AC的中点.
(2010•抚州模拟)在斜三棱柱ABC-A1B1C1中,AB=BC=2,∠ABC=120°,又顶点A1在底面ABC上的射影落在AC上,侧棱AA1与底面ABC成60°角,D为AC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
 已知斜三棱柱ABC-A1B1C1,∠BCA=90°,AC=BC=2,A1在底面ABC上的射影恰为AC的中点D,E为AB的中点,BA1⊥AC1.
已知斜三棱柱ABC-A1B1C1,∠BCA=90°,AC=BC=2,A1在底面ABC上的射影恰为AC的中点D,E为AB的中点,BA1⊥AC1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com