
【题目】4月23日是“世界读书日”,某中学在此期间开展了一系列的读书教育活动,为了解本校学生课外阅读情况,学校随机抽取了100名学生对其课外阅读时间进行调查,下面是根据调查结果绘制的学生日均课外阅读时间(单位:min)的频率分布直方图,若将日均课外阅读时间不低于60 min的学生称为“书虫”,低于60 min的学生称为“懒虫”,

(1)求x的值并估计全校3 000名学生中“书虫”大概有多少名学生?(将频率视为概率)
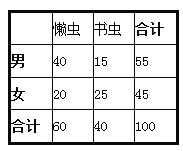
(2)根据已知条件完成下面2×2的列联表,并判断能否在犯错误的概率不超过0.01的前提下认为“书虫”与性别有关:

【答案】(1)x=0.025,1200人;(2)见解析.
【解析】试题分析:(1)由直方图,易知x=0.025,“书虫”大概有1200人;(2)完成表格,K2=≈8.249.由8.249>6.635,故在犯错误的概率不超过0.01的前提下认为“读书迷”与性别有关.
试题解析:
(1)由已知可得:(0.01+0.02+0.03+x+0.015)×10=1,可得x=0.025
因为(0.025+0.015)×10=0. 4,将频率视为概率,由此可以估算出全校3000名学生中“书虫”大概有1200人.
(2)完成下面的2×2列联表如下:
K2=≈8.249.
由8.249>6.635,故在犯错误的概率不超过0.01的前提下认为“读书迷”与性别有关.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源: 题型:
【题目】若平面点集![]() 满足:任意点
满足:任意点![]() ,存在
,存在![]() ,都有
,都有![]() ,则称该点集
,则称该点集![]() 是“
是“![]() 阶聚合”点集。现有四个命题:
阶聚合”点集。现有四个命题:
①若![]() ,则存在正数
,则存在正数![]() ,使得
,使得![]() 是“
是“![]() 阶聚合”点集;
阶聚合”点集;
②若![]() ,则
,则![]() 是“
是“![]() 阶聚合”点集;
阶聚合”点集;
③若![]() ,则
,则![]() 是“2阶聚合”点集;
是“2阶聚合”点集;
④若![]() 是“
是“![]() 阶聚合”点集,则
阶聚合”点集,则![]() 的取值范围是
的取值范围是![]() .
.
其中正确命题的序号为( )
A. ①④ B. ②③ C. ①② D. ③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知梯形![]() 与梯形
与梯形![]() 全等,
全等, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 中点.
中点.

(Ⅰ)证明: ![]() 平面
平面![]()
(Ⅱ)点![]() 在线段
在线段![]() 上(端点除外),且
上(端点除外),且![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC为等腰直角三角形, ![]() ,
, ![]() ,
, ![]() 分别是边
分别是边![]() 和
和![]() 的中点,现将
的中点,现将![]() 沿
沿![]() 折起,使平面
折起,使平面![]() ,
, ![]() 分别是边
分别是边![]() 和
和![]() 的中点,平面
的中点,平面![]() 与
与![]() ,
, ![]() 分别交于
分别交于![]() ,
, ![]() 两点.
两点.
(1)求证: ![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)求![]() 的长.
的长.
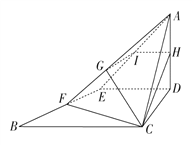
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角坐标系![]() 中,椭圆
中,椭圆![]() 的上焦点为
的上焦点为![]() ,椭圆
,椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点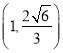 .
.
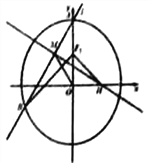
(1)求椭圆![]() 的方程.
的方程.
(2)设过椭圆![]() 的上顶点
的上顶点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于点
交于点![]() (
(![]() 不在
不在![]() 轴上),垂直于
轴上),垂直于![]() 的直线与
的直线与![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,且
,且![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数(x)=xlnx,g(x)=ax3-![]() .
.
(Ⅰ)求函数(x)的单调递增区间和最小值;
(Ⅱ)若函数y= (x)与函数y =g(x)的图象在交点处存在公共切线,求实数a的值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 、
、![]() 为常数).若函数
为常数).若函数![]() 与
与![]() 的图象在
的图象在![]() 处相切,
处相切,
(Ⅰ)求![]() 的解析式;
的解析式;
(Ⅱ)设函数![]()
![]() ,若
,若![]() 在
在![]() 上的最小值为
上的最小值为![]() ,求实数
,求实数![]() 的值;
的值;
(Ⅲ)设函数![]() ,若
,若![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com