
从 ,六个数字中任取两个奇数和两个偶数,组成没有重复数字的四位奇数,有多少种取法
,六个数字中任取两个奇数和两个偶数,组成没有重复数字的四位奇数,有多少种取法
A. | B. | C. | D. |
B
解析试题分析:从0,2,4这3个偶数数字中任选2个,分为以下两类:
一类:不含有0,即选取2,4时只有一种方法,再从1,3,5这3个数字中任取2个数字共有 种方法,从选取的两个奇数中任取一个放在个位上有
种方法,从选取的两个奇数中任取一个放在个位上有 种方法,其余3个数字全排列有3! 种方法,
种方法,其余3个数字全排列有3! 种方法,
由乘法原理可得:共有 种方法;另一类:含有数字0,再从2,4两个数字中任选
种方法;另一类:含有数字0,再从2,4两个数字中任选
一个共有 =2种选法,再从1,3,5这3个数字中任取2个数字共有
=2种选法,再从1,3,5这3个数字中任取2个数字共有 种方法,从选取的两个
种方法,从选取的两个
奇数中任取一个放在个位上有 种方法,数字0只能放在十位或百位上有
种方法,数字0只能放在十位或百位上有 种方法,剩下的两个数字
种方法,剩下的两个数字
有 种方法,由乘法原理可得:共有
种方法,由乘法原理可得:共有 种方法.
种方法.
由分类加法原理可得:满足题意的没有重复数字的四位奇数共有36+48=84种方法.选B.
考点:排列、组合及简单计数问题.
点评:本题综合考查了对分类加法原理、分步乘法原理、排列及组合的意义理解及其计算公式的应用,并且注意特殊位置(个位)特殊元素(0)优先考虑的方法的应用.


科目:高中数学 来源: 题型:单选题
若矩阵 满足下列条件:①每行中的四个数所构成的集合均为
满足下列条件:①每行中的四个数所构成的集合均为 ;②四列中至少有两列的上下两数是相同的.则这样的不同矩阵的个数为( )
;②四列中至少有两列的上下两数是相同的.则这样的不同矩阵的个数为( )
| A.48 | B.72 | C.168 | D.312 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
记者要为5名志愿者和他们帮助的2位老人拍照,要求排成一排,2位老人相邻,不同的排法共有( )
| A.1440种 | B.960种 |
| C.720种 | D.480种 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
记者要为5名志愿者和他们帮助的2位老人拍照,要求排成一排,2位老人相邻但不排在两端,不同的排法共有( )
| A.1440种 | B.960种 | C.720种 | D.480种 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
将5列车停在5条不同的轨道上,其中列车甲不停在第一轨道上,列车乙不停在第二轨道上,则不同的停放方法有 ( )
| A.70种 | B.72种 | C.76种 | D.78种 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
现需编制一个八位的序号,规定如下:序号由4个数字和2个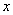 、1个
、1个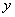 、1个
、1个 组成;2个
组成;2个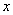 不能连续出现,且
不能连续出现,且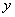 在
在 的前面;数字在1、2、4、8之间选取,可重复选取,且四个数字之积为8.则符合条件的不同的序号种数有( )
的前面;数字在1、2、4、8之间选取,可重复选取,且四个数字之积为8.则符合条件的不同的序号种数有( )
| A.12600 | B.6300 | C.5040 | D.2520 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com