练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    设函数f(x)=ax2+8x+3?(a∈R).?

    (1)若g(x)=xf(x),f(x)与g(x)在x为某值时,都取得极值,求a的值.

    (2)对于给定的负数a,有一个最大的正数M(a),使得x∈［0,M(a)］时,恒有|f(x)|≤5.

    求:①M(a)的表达式;

    ②M(a)的最大值及相应的a值.

    解析:(1)易知a≠0,f(x)在x=-处取得极值.?

    ∵g(x)=ax3+8x2+3x,?

    ∴g′(x)=3ax2+16x+3.?

    由题意得

    3a(-)2+16(-)+3=0,??

    ∴a=.?

    (2)∵a＜0,f(x)=a(x+)2+3-,

    ∴f(x)max=3-.?

    图(1)

             图(2)??

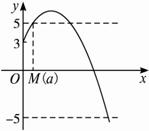
    如图(1),当3-＞5,即-8＜a＜0时,要使|f(x)|≤5在x∈［0,M(a)］上恒成立,而M(a)要最大,∴M(a)只能是方程ax2+8x+3=5的较小根.?

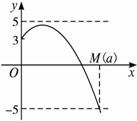
    如图(2),当3-≤5即a≤-8时,同样道理M(a)只能是方程ax2+8x+3=?-5?的较大根.?

    综上,得M(a)=?

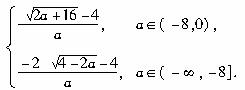
    当a∈(-8,0)时,M(a)=

    当a∈(-∞,-8］时,M(a)=

    ∴当且仅当a=-8时,M(a)有最大值.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    设函数f(x)=ax+
    a+1
    x
         (a＞0)    ，g（x）=4-x，已知满足f（x）=g（x）的x有且只有一个．
    （Ⅰ）求a的值；
    （Ⅱ）若f(x)+
    m
    x
    ＞1    对一切x＞0恒成立，求m的取值范围；
    （Ⅲ）若函数h（x）=k-f（x）-g（x）（k∈R）在[m，n]上的值域为[m，n]（其中n＞m＞0），求k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设函数f(x)=ax-
    bx
    ，曲线y=f（x）在点（2，f（2））处的切线方程为7x-4y-12=0，
    （1）求y=f（x）的解析式，并求其单调区间；
    （2）用阴影标出曲线y=f（x）与此切线以及x轴所围成的图形，并求此图形的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设函数f(x)=
    ax-1x+1
    ；其中a∈R    ．
    （Ⅰ）解不等式f（x）≤1；
    （Ⅱ）求a的取值范围，使f（x）在区间（0，+∞）上是单调减函数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设函数f(x)=ax-
    bx
    ，曲线y=f（x）在点（2，f（2））处的切线方程为7x-4y-12=0．
    （1）求f（x）的解析式；
    （2）讨论函数f（x）的单调性．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设函数f(x)=ax-
    bx
    ，曲线y=f（x）在点（2，f（2））处的切线方程为7x-4y-12=0．
    （1）求f（x）的解析式；
    （2）求函数f（x）的单调区间．

    查看答案和解析>>

    同步练习册答案