
【题目】将集合![]() 中的元素作全排列,使得除了最左端的一个数之外,对于其余的每个数
中的元素作全排列,使得除了最左端的一个数之外,对于其余的每个数![]() ,在
,在![]() 的左边某个位置上总有一个数与
的左边某个位置上总有一个数与![]() 之差的绝对值为1.则满足条件的排列个数为____________.
之差的绝对值为1.则满足条件的排列个数为____________.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图所示,在直三棱柱![]() 中,
中,![]() ,
,![]() 平面
平面![]() ,D为AC的中点.
,D为AC的中点.
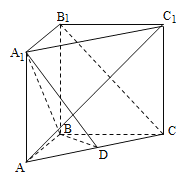
(1)求证:![]() 平面
平面![]() ;
;
(2)求证:![]() 平面
平面![]() ;
;
(3)设E是![]() 上一点,试确定E的位置使平面
上一点,试确定E的位置使平面![]() 平面BDE,并说明理由.
平面BDE,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在测试中,客观题难度的计算公式为![]() ,其中
,其中![]() 为第
为第![]() 题的难度,
题的难度,![]() 为答对该题的人数,
为答对该题的人数,![]() 为参加测试的总人数.现对某校高三年级120名学生进行一次测试,共5道客观题.测试前根据对学生的了解,预估了每道题的难度,如下表所示:
为参加测试的总人数.现对某校高三年级120名学生进行一次测试,共5道客观题.测试前根据对学生的了解,预估了每道题的难度,如下表所示:
题号 | 1 | 2 | 3 | 4 | 5 |
考前预估难度 | 0.9 | 0.8 | 0.7 | 0.6 | 0.4 |
测试后,从中随机抽取了10名学生,将他们编号后统计各题的作答情况,如下表所示(“√”表示答对,“×”表示答错):
学生编号 | 1 | 2 | 3 | 4 | 5 |
1 | × | √ | √ | √ | √ |
2 | √ | √ | √ | √ | × |
3 | √ | √ | √ | √ | × |
4 | √ | √ | √ | × | × |
5 | √ | √ | √ | √ | √ |
6 | √ | × | × | √ | × |
7 | × | √ | √ | √ | × |
8 | √ | × | × | × | × |
9 | √ | √ | × | × | × |
10 | √ | √ | √ | √ | × |
(1)根据题中数据,将抽样的10名学生每道题实测的答对人数及相应的实测难度填入下表,并估计这120名学生中第5题的实测答对人数:
题号 | 1 | 2 | 3 | 4 | 5 |
实测答对人数 | |||||
实测难度 |
(2)从编号为1到5的5人中随机抽取2人,求恰好有1人答对第5题的概率;
(3)定义统计量![]() ,其中
,其中![]() 为第
为第![]() 题的实测难度,
题的实测难度,![]() 为第
为第![]() 题的预估难度(
题的预估难度().规定:若
![]() ,则称该次测试的难度预估合理,否则为不合理.判断本次测试的难度预估是否合理.
,则称该次测试的难度预估合理,否则为不合理.判断本次测试的难度预估是否合理.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于![]() 的函数
的函数![]() ,
,
(I)试求函数![]() 的单调区间;
的单调区间;
(II)若![]() 在区间
在区间![]() 内有极值,试求a的取值范围;
内有极值,试求a的取值范围;
(III)![]() 时,若
时,若![]() 有唯一的零点
有唯一的零点![]() ,试求
,试求![]() .(注:
.(注:![]() 为取整函数,表示不超过
为取整函数,表示不超过![]() 的最大整数,如
的最大整数,如![]() ;以下数据供参考:
;以下数据供参考:![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com