Question

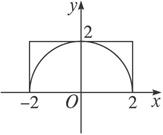
如图3-3-16所示，在长为4、宽为2的矩形中有一以矩形的长为直径的半圆，试用随机模拟法近似计算半圆的面积，并估计π的值.

         图3-3-16

Answer 1

思路分析：本题考查几何概型的计算公式及均匀随机数的产生方法.

解：设事件A“随机向矩形内投点，所投的点在半圆内”.

第一步,用计数器n记录做了多少次投点试验，用计数器m记录其中有多少次落在(x,y)满足的条件x²+y²＜4(即点落在半圆内).首先置n=0,m=0；

第二步,用变换rand()*4-2产生-2～2之间的均匀随机数x表示所投的点的横坐标；用变换rand()*2产生0～2之间的均匀随机数y表示所投点的纵坐标；

第三步,判断点是否落在阴影部分，即是否满足x²+y²＜4.如果是，则计数器m的值加1，即m=m+1.如果不是，m的值保持不变；

第四步,表示随机试验次数的计数器n的值加1，即n=n+1.如果还要继续试验，则返回第二步继续执行，否则，程序结束.

程序结束后事件A发生的频率作为事件A的概率的近似值.

设半圆的面积为S，矩形的面积为8，由几何概率计算公式得P(A)=.

所以≈.

所以S≈即为阴影部分面积的近似值.

由面积公式得S=2π，

所以π≈.