
����Ŀ������Բ����![]() ����ѧ��չʷ�ϳ��ֹ�������д���������������ѷ�����.��������������Ҳ����ͨ��������������������
����ѧ��չʷ�ϳ��ֹ�������д���������������ѷ�����.��������������Ҳ����ͨ��������������������![]() ��ֵ�����鲽�����£�������߶��꼶 500��ͬѧÿ����С��Ƭ�����д��һ��ʵ����
��ֵ�����鲽�����£�������߶��꼶 500��ͬѧÿ����С��Ƭ�����д��һ��ʵ����![]() ��������Ƭ�ϵ�
��������Ƭ�ϵ�![]() ����1������������Σ��˿�Ƭ�Ͻ�����ͳ���Ͻ��Ŀ�Ƭ������Ϊ
����1������������Σ��˿�Ƭ�Ͻ�����ͳ���Ͻ��Ŀ�Ƭ������Ϊ![]() ���ܸ���ͳ����
���ܸ���ͳ����![]() ����
����![]() ��ֵ.���籾�������ͳ�ƽ����
��ֵ.���籾�������ͳ�ƽ����![]() ����ô���Թ���
����ô���Թ���![]() ��ֵԼΪ�� ��
��ֵԼΪ�� ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
���𰸡�A
��������������500�Զ�С��l����ʵ���ԣ�x��y������![]() �����Ϊ1������������1����������������ߵ����ԣ�x��y��������x2+y2��1��
�����Ϊ1������������1����������������ߵ����ԣ�x��y��������x2+y2��1��![]() ��x+y��1�����Ϊ1��
��x+y��1�����Ϊ1��![]() ���ɴ��ܹ��Ʀе�ֵ��
���ɴ��ܹ��Ʀе�ֵ��
��⣺�����⣬500�Զ�С��l����ʵ���ԣ�x��y������![]() �����Ϊ1��
�����Ϊ1��
����������1����������������ߵ����ԣ�x��y��������![]() ��
��![]() ��
��
��x2+y2��1����![]() ��
��
���Ϊ1��![]() ��
��
��Ϊͳ����������l ����������������ߵ����ԣ�x��y�� �ĸ���m=113��
����![]() =1��
=1��![]() �����Ԧ�=
�����Ԧ�=![]() ��
��
�ʴ�Ϊ��A



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() ��
��
��1��������![]() ��
��![]() �������߷���Ϊ
�������߷���Ϊ![]() ����ʵ��
����ʵ��![]() ��ֵ��
��ֵ��
��2����![]() �����������������ȵ�����
�����������������ȵ�����![]() ��
��![]() ������
������![]() ���������ʵ��
���������ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3������![]() �ϴ���һ��
�ϴ���һ��![]() ��ʹ��
��ʹ��![]() ��������ʵ��
��������ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
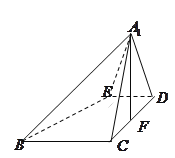
����Ŀ����֪������![]() �ı߳�Ϊ
�ı߳�Ϊ![]() ����
����![]() �ضԽ���
�ضԽ���![]() ����ʹƽ��
����ʹƽ��![]() ƽ��
ƽ��![]() ���õ���ͼ��ʾ������
���õ���ͼ��ʾ������![]() ����
����![]() Ϊ
Ϊ![]() �ߵ��е㣬
�ߵ��е㣬![]() �ֱ�Ϊ
�ֱ�Ϊ![]() �ϵĶ��㣨�������˵㣩����
�ϵĶ��㣨�������˵㣩����![]() ����
����![]() ��������
��������![]() �����ȡ�����ֵʱ������
�����ȡ�����ֵʱ������![]() ��������İ뾶Ϊ_______.
��������İ뾶Ϊ_______.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ��������Ϊ
��������Ϊ![]() ��������
��������![]() ����Բ
����Բ![]() �ڵ�һ�����Ľ���Ϊ
�ڵ�һ�����Ľ���Ϊ![]() ��
��
��1��������![]() ��
��![]() �ķ��̣�
�ķ��̣�
��2����������![]() ����ȡһ��
����ȡһ��![]() ���ڵ�
���ڵ�![]() ����������
����������![]() ������
������![]() ������Բ
������Բ![]() �ϴ����������ֱ��
�ϴ����������ֱ��![]() �Գƣ����
�Գƣ����![]() ���������ȡֵ��Χ��
���������ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2018��1��26�գ�����ʡ���������칫������������ʡ���ڲ���ҵ������ȫ�������̵�ʵʩ���������������16����ѧʳ�õġ����������ϸ��ԡ��͡�ʳƷ��ȫ��������������.��10����Ϊ����ȫʳ�á�������7�����µ�Ϊ�����ĸ�ʳ�á�.������4�����¿���Ϊ��ȡ��ʳ�á������д�ѧʳ�õ�������7~10��֮�䣬���±����¼�����ǵ����������

��1���ִ�16����ѧʳ���������ȡ3������������1�����ֲ�����9�ֵĸ��ʣ�
��2������16����ѧʳ���������ݹ��ƴ�ѧʳ�õľ�Ӫ���ʣ�����ȫ���Ĵ�ѧʳ����ѡ3������![]() ��ʾ�鵽���ֲ�����9�ֵ�ʳ�ø�������
��ʾ�鵽���ֲ�����9�ֵ�ʳ�ø�������![]() �ķֲ��м���ѧ����.
�ķֲ��м���ѧ����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
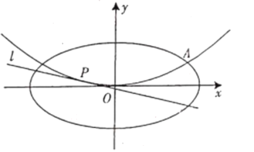
����Ŀ�������һ�����Ƿ־�����ֱ�ߵ���ͷ������һ����Խʱ�յ�������������������������һ��Ҳ��Ը����.��ͼ1��ʾ��������![]() �У�
�У�![]() //
//![]() ����
����![]() ��
��![]() ���ֱ��ӳ��������ڵ�
���ֱ��ӳ��������ڵ�![]() ����
����![]() Ϊ�߶�
Ϊ�߶�![]() �ϵ�һ�㣬��
�ϵ�һ�㣬��![]() ��
��![]() ����
����![]() ��λ�ã�ʹ
��λ�ã�ʹ![]() ����ͼ2��ʾ��
����ͼ2��ʾ��
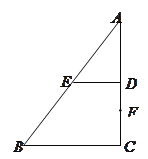
��1����֤��![]() ��
��
��2����![]() ��
��![]() ������
������![]() �����Ϊ
�����Ϊ![]() ��������
��������![]() �ı����.
�ı����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������һ����һ����ö�ʵؾ��ȵ������������ӣ��ֱ�۲�����ϵ�����.

��1���ñ����ʾ��������п��ܽ����
��2���о������¼������������㣺A=������������ͬ����B=����������֮�͵���5����C=����ɫ���ӵ�����Ϊ2��.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com