分析:(1)连接CE交AD于O,连接OF.因为CE,AD为△ABC中线,所以O为△ABC的重心,
==.由此能够证明C
1E∥平面ADF.
(2)当BM=1时,平面CAM⊥平面ADF.在直三棱柱ABC-A
1B
1C
1中,先证出AD⊥平面B
1BCC
1.再证明当BM=1时,平面CAM⊥平面ADF.
解答:解:(1)连接CE交AD于O,连接OF.
因为CE,AD为△ABC中线,
所以O为△ABC的重心,
==.
从而OF∥C
1E.…(3分)
OF?面ADF,C
1E?平面ADF,
所以C
1E∥平面ADF.…(6分)
(2)当BM=1时,平面CAM⊥平面ADF.
在直三棱柱ABC-A
1B
1C
1中,
由于B
1B⊥平面ABC,BB
1?平面B
1BCC
1,
所以平面B
1BCC
1⊥平面ABC.
由于AB=AC,D是BC中点,所以AD⊥BC.
又平面B
1BCC
1∩平面ABC=BC,
所以AD⊥平面B
1BCC
1.
而CM?平面B
1BCC
1,于是AD⊥CM.…(9分)
因为BM=CD=1,BC=CF=2,所以Rt△CBM≌Rt△FCD,
所以CM⊥DF. …(11分)
DF与AD相交,所以CM⊥平面ADF.
CM?平面CAM,所以平面CAM⊥平面ADF.…(13分)
当BM=1时,平面CAM⊥平面ADF.…(14分)
点评:本小题主要考查空间线面关系、几何体的体积等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力.

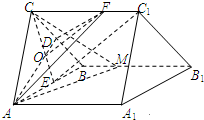 (2012•泰州二模)如图,三棱柱ABC-A1B1C1中,D、E分别是棱BC、AB的中点,点F在棱CC1上,已知AB=AC,AA1=3,BC=CF=2.
(2012•泰州二模)如图,三棱柱ABC-A1B1C1中,D、E分别是棱BC、AB的中点,点F在棱CC1上,已知AB=AC,AA1=3,BC=CF=2.

 名校课堂系列答案
名校课堂系列答案