
分析 运用反证法,假设结论成立,再经过推理与证明,即可得出正确的结论.
解答 解:假设甲说的是实话,则“是乙不小心闯的祸”正确,丙、丁说的都是实话,
这与四个小朋友中只有一个人说了实话矛盾,假设错误;
假设乙说的是实话,则“是丙闯的祸”正确,丁说的也是实话,
这与四个小朋友中只有一个人说了实话矛盾,假设错误;
假设丙说的是实话,则“乙说的不是实话”正确,甲、乙、丁说的都是不实话,
得出丁闯的祸,符合题意;
假设丁说的是实话,则“反正不是我闯的祸”正确,甲、乙、丁中至少有一人说的是实话,
这与四个小朋友中只有一个人说了实话矛盾,假设错误.
故答案为:丙.
点评 本题考查了推理与证明的应用问题,是基础题目.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-6]∪[2,+∞) | B. | (-∞,-4)∪(4,+∞) | C. | [2,+∞) | D. | [-6,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
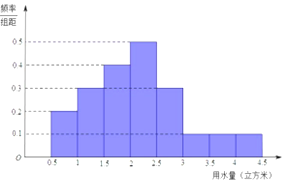 某市为鼓励居民节约用水,拟实行阶梯水价,每人用水量中不超过w 立方米按2 元/立方米收费,超出w 立方米但不高于w+2 的部分按4 元/立方米收费,超出w+2 的部分按8 元/立方米收费,从该市随机调查了10000 位居民,获得了他们某月的用水量数据,整理得到如图所示频率分布直方图:
某市为鼓励居民节约用水,拟实行阶梯水价,每人用水量中不超过w 立方米按2 元/立方米收费,超出w 立方米但不高于w+2 的部分按4 元/立方米收费,超出w+2 的部分按8 元/立方米收费,从该市随机调查了10000 位居民,获得了他们某月的用水量数据,整理得到如图所示频率分布直方图:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
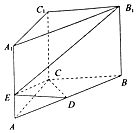 如图所示,在直三棱柱ABC-A1B1C1中,底面ABC是等腰直角三角形,且斜边AB=2$\sqrt{2}$,侧棱AA1=4,点D为AB的中点,点E在线段AA1上,AE=λAA1(λ∈R).
如图所示,在直三棱柱ABC-A1B1C1中,底面ABC是等腰直角三角形,且斜边AB=2$\sqrt{2}$,侧棱AA1=4,点D为AB的中点,点E在线段AA1上,AE=λAA1(λ∈R).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com