
【题目】正方体![]() 的棱长为1,
的棱长为1,![]() 分别为
分别为![]() 的中点.有下述四个结论:①直线
的中点.有下述四个结论:①直线![]() 与直线
与直线![]() 垂直;②直线
垂直;②直线![]() 与平面
与平面![]() 平行;③平面
平行;③平面![]() 截正方体所得的截面面积为
截正方体所得的截面面积为![]() ;④直线
;④直线![]() 与直线
与直线![]() 所成角的正切值为
所成角的正切值为![]() ;其中所有正确结论的编号是( )
;其中所有正确结论的编号是( )

A.②③B.②④C.①③D.③④
【答案】A
【解析】
①利用线线平行,将![]() 与
与![]() 的位置关系转换为判断
的位置关系转换为判断![]() 与
与![]() 的位置关系;②作出辅助线:取
的位置关系;②作出辅助线:取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() ,然后利用面面平行判断;③作出截面,再根据梯形的面积公式求需要的线段长;④利用平移的思想,将两条异面直线平移在同一个平面内,然后结合余弦定理求夹角的余弦值,再转化为正切值.
,然后利用面面平行判断;③作出截面,再根据梯形的面积公式求需要的线段长;④利用平移的思想,将两条异面直线平移在同一个平面内,然后结合余弦定理求夹角的余弦值,再转化为正切值.
对于①,因为![]() ,若
,若![]() ,则
,则![]() ,从图中可以看出,
,从图中可以看出,
![]() 与
与![]() 相交,但不垂直,所以①错误;
相交,但不垂直,所以①错误;
对于②,如图所示,取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() ,则有
,则有![]() ,
,![]() ,
,
因为![]() ,
,![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
又因为![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,即②正确;
,即②正确;

对于③,如图所示,连接![]() ,
,![]() ,延长
,延长![]() ,
,![]() 交于点
交于点![]() ,
,
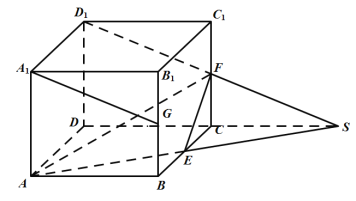
因为![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,所以
的中点,所以![]() ,所以
,所以![]() 、
、![]() 、
、![]() 、
、![]() 四点共面,所以截面即为梯形
四点共面,所以截面即为梯形![]() .
.
因为![]() ,所以
,所以![]() ,即
,即![]() ,所以
,所以![]()
又![]() ,所以
,所以![]() 即
即![]() ,
,![]() ,
,
所以等腰△![]() 的高
的高![]() ,梯形
,梯形![]() 的高为
的高为![]() ,
,
所以梯形![]() 的面积为
的面积为![]() ,所以③正确;
,所以③正确;
对于④,因为![]() ,所以直线
,所以直线![]() 与直线
与直线![]() 所成角即为所求.
所成角即为所求.
在三角形![]() 中,
中,![]() ,由余弦定理得,
,由余弦定理得, ,
,
因为直线的夹角范围为![]() ,
,![]() ,所以直线
,所以直线![]() 与直线
与直线![]() 所成角的正切值为3.所以④错误.
所成角的正切值为3.所以④错误.
故选:![]() .
.


科目:高中数学 来源: 题型:
【题目】已知过点![]() 的圆
的圆![]() 的圆心
的圆心![]() 在
在![]() 轴的非负半轴上,且圆
轴的非负半轴上,且圆![]() 截直线
截直线![]() 所得弦长为
所得弦长为![]() .
.
(1)求![]() 的标准方程;
的标准方程;
(2)若过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 交圆
交圆![]() 于
于![]() 、
、![]() 两点,若
两点,若![]() 的面积为
的面积为![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解我市参加2018年全国高中数学联赛的学生考试结果情况,从中选取60名同学将其成绩(百分制,均为正数)分成![]() 六组后,得到部分频率分布直方图(如图),观察图形,回答下列问题:
六组后,得到部分频率分布直方图(如图),观察图形,回答下列问题:
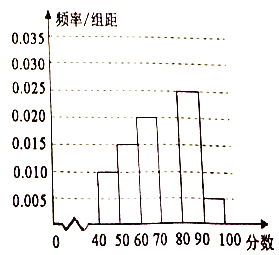
(1)求分数在![]() 内的频率,并补全这个频率分布直方图;
内的频率,并补全这个频率分布直方图;
(2)根据频率分布直方图,估计本次考试成绩的众数、均值;
(3)根据评奖规则,排名靠前10%的同学可以获奖,请你估计获奖的同学至少需要所少分?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某上市公司股票在30天内每股的交易价格P(元)关于时间t(天)的函数关系为 ,该股票在30天内的日交易量Q(万股)关于时间t(天)的函数为一次函数,其图象过点
,该股票在30天内的日交易量Q(万股)关于时间t(天)的函数为一次函数,其图象过点![]() 和点
和点![]() .
.
(1)求出日交易量Q(万股)与时间t(天)的一次函数关系式;
(2)用y(万元)表示该股票日交易额,写出y关于t的函数关系式,并求在这30天内第几天日交易额最大,最大值为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现代社会对破译密码的难度要求越来越高,有一处密码把英文的明文(真实名)按字母分解,其中英文a,b,c……,z这26个字母,依次对应1,2,3……,26这26个正整数.(见下表)
a | b | c | d | e | f | g | h | i | j | k | l | m |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
n | o | p | q | r | s | t | u | v | w | x | y | z |
14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
用如下变换公式: 将明文转换成密码.如
将明文转换成密码.如![]() .即h变成q;再如:
.即h变成q;再如:![]() ,即y变成m;按上述变换规则,若将明文译成的密码是gano,那么原来的明文是______________.
,即y变成m;按上述变换规则,若将明文译成的密码是gano,那么原来的明文是______________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了解所经销商品的使用情况,随机问卷50名使用者,然后根据这50名的问卷评分数据,统计得到如图所示的频率布直方图,其统计数据分组区间为[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].

(1)求频率分布直方图中a的值并估计这50名使用者问卷评分数据的中位数;
(2)从评分在[40,60)的问卷者中,随机抽取2人,求此2人评分都在[50,60)的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=4x,其焦点为F,直线过点P(﹣2,0)
(1)若直线l与抛物线C有且仅有一个公共点,求l的方程;
(2)若直线l与抛物线交于不同的两点A、B,求|FA|+|FB|的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】石嘴山市第三中学高三年级统计学生的最近20次数学周测成绩(满分150分),现有甲乙两位同学的20次成绩如茎叶图所示:

(1)根据茎叶图求甲乙两位同学成绩的中位数,并将同学乙的成绩的频率分布直方图填充完整;
(2)根据茎叶图比较甲乙两位同学数学成绩的平均值及稳定程度(不要求计算出具体值,给出结论即可);
(3)现从甲乙两位同学的不低于140分的成绩中任意选出2个成绩,记事件![]() 为“其中2个成绩分别属于不同的同学”,求事件
为“其中2个成绩分别属于不同的同学”,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆O:![]() ,直线l:
,直线l:![]() .
.
(1)若直线l与圆O相切,求k的值;
(2)若直线l与圆O交于不同的两点A,B,当![]() 为锐角时,求k的取值范围;
为锐角时,求k的取值范围;
(3)若![]() ,P是直线l上的动点,过P作圆O的两条切线PC,PD,切点为C,D,探究:直线CD是否过定点,若过定点,则求出该定点.
,P是直线l上的动点,过P作圆O的两条切线PC,PD,切点为C,D,探究:直线CD是否过定点,若过定点,则求出该定点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com