练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】下列叙述： ①函数 是奇函数；
    ②函数 的一条对称轴方程为 ；
    ③函数 ， ，则f（x）的值域为 ；
    ④函数 有最小值，无最大值．
    所有正确结论的序号是 ．

    【答案】②④
    【解析】解：①函数 ，显然f（﹣x）≠f（x），不是奇函数，故错误； ②f（﹣ ）=﹣1， 的一条对称轴方程为 ，故正确；
    ③函数 ， ，2x+ ，则f（x）的值域为[﹣1， ]，故错误；
    ④函数 ，f（x）≥4，有最小值，无最大值，故正确．
    所以答案是②④．
    【考点精析】本题主要考查了命题的真假判断与应用的相关知识点，需要掌握两个命题互为逆否命题，它们有相同的真假性；两个命题为互逆命题或互否命题，它们的真假性没有关系才能正确解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，在△ABC中，已知B=45°，D是BC边上的一点，AD=4，AC=2 ，DC=2
    （1）求cos∠ADC
    （2）求AB．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆C：（x﹣1）2+（y﹣2）2=4．
    （1）求直线2x﹣y+4=0被圆C所截得的弦长；
    （2）求过点M（3，1）的圆C的切线方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知直棱柱ABC﹣A1B1C1中，AC=BC=CC1= AB，E是线段CC1的中点，连接AE，B1E，AB1 ， B1C，BC1 ， 得到的图形如图所示． （Ⅰ）证明BC1⊥平面AB1C；
    （Ⅱ）求二面角E﹣AB1﹣C的大小．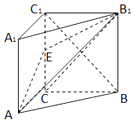

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设x，y满足约束条件： ；则z=x﹣2y的取值范围为 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知
    （1）求函数f（x）的最小正周期和最大值，并求出x为何值时，f（x）取得最大值；
    （2）求函数f（x）在[﹣2π，2π]上的单调增区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若先将函数y= sin（x﹣ ）+cos（x﹣ ）图象上各点的纵坐标不变，横坐标缩短到原来的 倍，再将所得图象向左平移 个单位，所得函数图象的一条对称轴的方程是（ ）
    A.x=
    B.x=
    C.x=
    D.x=

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某港口的水深y（米）是时间t（0≤t≤24，单位：小时）的函数，下面是每天时间与水深的关系表：

    t

    0

    3

    6

    9

    12

    15

    18

    21

    24

    y

    10

    13

    9.9

    7

    10

    13

    10.1

    7

    10

    经过长期观测，y=f（t）可近似的看成是函数y=Asinωt+b
    （1）根据以上数据，求出y=f（t）的解析式；
    （2）若船舶航行时，水深至少要11.5米才是安全的，那么船舶在一天中的哪几段时间可以安全的进出该港？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在棱长都相等的四面体P－ABC中，D、E、F分别是AB、BC、CA的中点，则下面四个结论中不成立的是 ( )
    A.BC∥平面PDF
    B.DF⊥平面PAE
    C.平面PDF⊥平面ABC
    D.平面PAE⊥平面ABC

    查看答案和解析>>

    同步练习册答案