练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某校对高一年级学生的数学成绩进行统计，全年级同学的成绩全部介于60分与100分之间，将他们的成绩数据绘制如图所示的频率分布直方图．现从全体学生中，采用分层抽样的方法抽取80名同学的试卷进行分析，则从成绩在[80，100]内的学生中抽取的人数为（ ）

    A.56
    B.32
    C.24
    D.18

    【答案】A
    【解析】解：根据频率分布直方图知，成绩在[80，100]内的频率为

    （0.04+0.03）×10=0.7，

    所以从中抽取的人数为

    80×0.7=56．

    所以答案是：A．

    【考点精析】通过灵活运用频率分布直方图，掌握频率分布表和频率分布直方图，是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式，可展示数据的分布情况.通过作图既可以从数据中提取信息，又可以利用图形传递信息即可以解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图所示是一个三棱台ABC－A′B′C′，试用两个平面把这个三棱台分成三部分，使每一部分都是一个三棱锥．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】△ABC的内角A，B，C的对边分别为a，b，c，已知sinB+sinA（sinC﹣cosC）=0，a=2，c= ，则C=（ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，正方体ABCD﹣A1B1C1D1中，E，F，H分别为A1B1 ， B1C1 ， CC1的中点．
    （Ⅰ）证明：BE⊥AH；
    （Ⅱ）在棱D1C1上是否存在一点G，使得AG∥平面BEF？若存在，求出点G的位置；若不存在，请说明理由．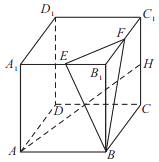

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】对于函数f（x），若存在区间A=[m，n]，使得{y|y=f（x），x∈A}=A，则称函数f（x）为“可等域函数”，区间A为函数f（x）的一个“可等域区间”．给出下列四个函数： ①f（x）=sin x；②f（x）=2x2﹣1；③f（x）=|1﹣2x|
    其中存在“可等域区间”的“可等域函数”为（ ）
    A.①
    B.②
    C.①②
    D.①②③

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知甲、乙两组数据如茎叶图所示，若它们的中位数相同，平均数也相同，则图中的m+n= ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}（n∈N*）是首项为20的等差数列，其公差d≠0，且a1 ， a4 ， a5成等比数列．
    （Ⅰ）求数列{an}的通项公式；
    （Ⅱ）设数列{an}的前n项和为Sn ， 当Sn＞0时，求n的最大值；
    （Ⅲ）设bn=5﹣ ，求数列{ }的前n项和Tn ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）= ．
    （1）当a=b=1时，求满足f（x）=3x的x的值；
    （2）若函数f（x）是定义在R上的奇函数，
    ①判断f（x）在R的单调性并用定义法证明；
    ②当x≠0时，函数g（x）满足f（x）[g（x）+2]= （3﹣x﹣3x），若对任意x∈R且x≠0，不等式g（2x）≥mg（x）﹣11恒成立，求实数m的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数ｆ（ｘ）＝-x3-2x2+4x，当x∈[-3,3]时，f（x）≥a有恒成立，则实数a的取值范围是（ ）
    A.（-3,11）
    B.[-33，+∞)
    C.(-∞，-33]
    D.[2,7]

    查看答案和解析>>

    同步练习册答案