
ЁОЬтФПЁПФГЗўзАГЇЩњВњвЛжжЗўзАЃЌУПМўЗўзАЕФГЩБОЮЊ40дЊЃЌГіГЇЕЅМлЮЊ60дЊЃЌИУГЇЮЊЙФРјЯњЪлЩЬЖЉЙКЃЌОіЖЈЕБвЛДЮЖЉЙКСПГЌЙ§100МўЪБЃЌУПЖрЖЉЙКвЛМўЃЌЖЉЙКЕФШЋВПЗўзАЕФГіГЇЕЅМлОЭНЕЕЭ0.02дЊЃЌИљОнЪаГЁЕїВщЃЌЯњЪлЩЬвЛДЮЖЉЙКСПВЛЛсГЌЙ§500МўЃЎ
ЃЈ1ЃЉЩшвЛДЮЖЉЙКСПЮЊxМўЃЌЗўзАЕФЪЕМЪГіГЇЕЅМлЮЊPдЊЃЌаДГіКЏЪ§P=fЃЈxЃЉЕФБэДяЪНЃЛ
ЃЈ2ЃЉЕБЯњЪлЩЬвЛДЮЖЉЙКЖрЩйМўЗўзАЪБЃЌИУЗўзАГЇЛёЕУЕФРћШѓзюДѓЃПВЂЧѓГізюДѓжЕЃЎ
ЁОД№АИЁП
ЃЈ1ЃЉНтЃКЩшвЛДЮЖЉЙКСПЮЊxМўЃЌЗўзАЕФЪЕМЪГіГЇЕЅМлЮЊPдЊЃЌ
ЕБ0ЃМxЁм100ЪБЃЌP=60
ЕБ100ЃМxЁм500ЪБЃЌ ![]()
Ыљвд 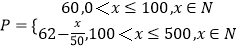
ЃЈ2ЃЉНтЃКЩшЯњЪлЩЬвЛДЮЖЉЙКСПЮЊxМўЃЌЙЄГЇЛёЕУЕФРћШѓЮЊyдЊЃЌдђга 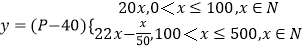
ЕБ0ЃМxЁм100ЧвxЁЪNЪБЃЌвзжЊx=100ЃЌyШЁЕУзюДѓжЕ2000дЊ
ЕБ100ЃМxЁм500ЧвxЁЪNЪБЃЌ ![]() ЃЌ
ЃЌ
дђДЫКЏЪ§дк100ЃМxЁм500ЧвxЁЪNЩЯЕндіЃЌЙЪx=500ЪБЃЌyШЁЕУзюДѓжЕ6000дЊЃЎ
Ёп6000ЃО2000ЃЌ
ЁрЕБЯњЪлЩЬвЛДЮЖЉЙК500МўЗўзАЪБЃЌИУЗўзАГЇЛёЕУЕФзюДѓРћШѓ6000дЊ
ЁОНтЮіЁПЃЈ1ЃЉРћгУЗжЖЮКЏЪ§жБНгСаГіКЏЪ§ЕФНтЮіЪНМДПЩЃЎЃЈ2ЃЉРћгУЃЈ1ЃЉСаГіРћШѓКЏЪ§ЃЌЗжБ№ЧѓНтЗжЖЮКЏЪ§ЕФзюжЕЃЌЭЦГіНсЙћМДПЩЃЎ


 бєЙтПЮЬУПЮЪБгХЛЏзївЕЯЕСаД№АИ
бєЙтПЮЬУПЮЪБгХЛЏзївЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖдгкШЮвтЪЕЪ§aЃЌbЃЌcЃЌdЃЌвдЯТЫФИіУќЬтжаЕФецУќЬтЪЧЃЈ ЃЉ
A.ШєaЃОbЃЌcЁй0дђacЃОbc
B.ШєaЃОbЃОoЃЌcЃОdдђacЃОbd
C.ШєaЃОbЃЌдђ ![]()
D.Шєac2ЃОbc2дђaЃОb
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
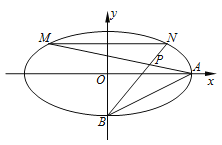
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌвбжЊЭждВ
жаЃЌвбжЊЭждВ![]() Й§Еу
Й§Еу![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЗжБ№ЮЊЭждВ
ЗжБ№ЮЊЭждВ![]() ЕФгвЁЂЯТЖЅЕуЃЌЧв
ЕФгвЁЂЯТЖЅЕуЃЌЧв![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓЭждВ![]() ЕФЗНГЬЃЛ
ЕФЗНГЬЃЛ
ЃЈ2ЃЉЩшЕу![]() дкЭждВ
дкЭждВ![]() ФкЃЌТњзужБЯп
ФкЃЌТњзужБЯп![]() ЃЌ
ЃЌ ![]() ЕФаБТЪГЫЛ§ЮЊ
ЕФаБТЪГЫЛ§ЮЊ![]() ЃЌЧвжБЯп
ЃЌЧвжБЯп![]() ЃЌ
ЃЌ ![]() ЗжБ№НЛЭждВ
ЗжБ№НЛЭждВ![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ ![]() ЃЎ
ЃЎ
(i) Шє![]() ЃЌ
ЃЌ ![]() Йигк
Йигк![]() жсЖдГЦЃЌЧѓжБЯп
жсЖдГЦЃЌЧѓжБЯп![]() ЕФаБТЪЃЛ
ЕФаБТЪЃЛ
(ii) ЧѓжЄЃК ![]() ЕФУцЛ§гы
ЕФУцЛ§гы![]() ЕФУцЛ§ЯрЕШЃЎ
ЕФУцЛ§ЯрЕШЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкРтГЄЮЊ1ЕФе§ЗНЬхABCDЉA1B1C1D1жаЃЌЕуEЃЌFЗжБ№ЪЧРтBCЃЌCC1ЕФжаЕуЃЌPЪЧВрУцBCC1B1ФквЛЕуЃЌШєA1PЁЮЦНУцAEFЃЌдђЯпЖЮA1PГЄЖШЕФШЁжЕЗЖЮЇЪЧ ЃЎ 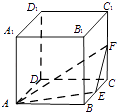
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
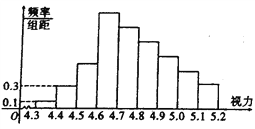
ЁОЬтФПЁПЭГМЦШЋЙњИпШ§бЇЩњЕФЪгСІЧщПіЃЌЕУЕНШчЭМЫљЪОЕФЦЕТЪЗжВМжБЗНЭМЃЌгЩгкВЛЩїНЋВПЗжЪ§ОнЖЊЪЇЃЌЕЋжЊЕРЧА4зщЕФЦЕТЪГЩЕШБШЪ§СаЃЌКѓ6зщЕФЦЕТЪГЩЕШВюЪ§Са.
ЃЈЂёЃЉЧѓГіЪгСІдк[4.7,4.8]ЕФЦЕТЪЃЛ
ЃЈЂђЃЉЯжДгШЋЙњЕФИпШ§бЇЩњжаЫцЛњЕиГщШЁ4ШЫЃЌгУ![]() БэЪОЪгСІдк[4.3,4.7]ЕФбЇЩњШЫЪ§ЃЌаДГі
БэЪОЪгСІдк[4.3,4.7]ЕФбЇЩњШЫЪ§ЃЌаДГі![]() ЕФЗжВМСаЃЌВЂЧѓГі
ЕФЗжВМСаЃЌВЂЧѓГі![]() ЕФЦкЭћгыЗНВю.
ЕФЦкЭћгыЗНВю.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§FЃЈxЃЉ=gЃЈxЃЉ+hЃЈxЃЉ=ex ЃЌ ЧвgЃЈxЃЉЃЌhЃЈxЃЉЗжБ№ЪЧRЩЯЕФХМКЏЪ§КЭЦцКЏЪ§ЃЌШєЖдШЮвтЕФxЁЪЃЈ0ЃЌ+ЁоЃЉЃЌВЛЕШЪНgЃЈ2xЃЉЁнahЃЈxЃЉКуГЩСЂЃЌдђЪЕЪ§aЕФШЁжЕЗЖЮЇЪЧЃЈ ЃЉ
A.ЃЈЉЁоЃЌ2 ![]() ]
]
B.ЃЈЉЁоЃЌ2 ![]() ЃЉ
ЃЉ
C.ЃЈЉЁоЃЌ2]
D.ЃЈЉЁоЃЌ2ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§fЃЈxЃЉ=Љ3x2+aЃЈ6ЉaЃЉx+cЃЎ
ЃЈ1ЃЉЕБc=19ЪБЃЌНтЙигкaЕФВЛЕШЪНfЃЈ1ЃЉЃО0ЃЛ
ЃЈ2ЃЉШєЙигкxЕФВЛЕШЪНfЃЈxЃЉЃО0ЕФНтМЏЪЧЃЈЉ1ЃЌ3ЃЉЃЌЧѓЪЕЪ§aЃЌcЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊХзЮяЯп![]() ЕФЖЅЕуЮЊдЕу
ЕФЖЅЕуЮЊдЕу![]() ЃЌНЙЕуЮЊдВ
ЃЌНЙЕуЮЊдВ![]() ЕФдВаФ
ЕФдВаФ![]() .ОЙ§Еу
.ОЙ§Еу![]() ЕФжБЯп
ЕФжБЯп![]() НЛХзЮяЯп
НЛХзЮяЯп![]() гк
гк![]() СНЕуЃЌНЛдВ
СНЕуЃЌНЛдВ![]() гк
гк![]() СНЕуЃЌ
СНЕуЃЌ ![]() дкЕквЛЯѓЯоЃЌ
дкЕквЛЯѓЯоЃЌ ![]() дкЕкЫФЯѓЯо.
дкЕкЫФЯѓЯо.
ЃЈ1ЃЉЧѓХзЮяЯп![]() ЕФЗНГЬЃЛ
ЕФЗНГЬЃЛ
ЃЈ2ЃЉЪЧЗёДцдкжБЯп![]() ЃЌЪЙ
ЃЌЪЙ![]() ЪЧ
ЪЧ![]() гы
гы![]() ЕФЕШВюжаЯюЃПШєДцдкЃЌЧѓжБЯп
ЕФЕШВюжаЯюЃПШєДцдкЃЌЧѓжБЯп![]() ЕФЗНГЬЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ЕФЗНГЬЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгаМзЁЂввСНИіАрНјааЪ§бЇПМЪдЃЌАДееДѓгкЕШгк120ЗжЮЊгХауЃЌ120ЗжвдЯТЮЊЗЧгХауЭГМЦГЩМЈКѓЃЌЕУЕНШчЯТ![]() СаСЊБэЃКЃЈЕЅЮЛЃКШЫЃЉ.
СаСЊБэЃКЃЈЕЅЮЛЃКШЫЃЉ.

вбжЊдкШЋВП105ШЫжаЫцЛњГщШЁ1ШЫГЩМЈЪЧгХауЕФИХТЪЮЊ![]() .
.
ЃЈ1ЃЉЧыЭъГЩЩЯУцЕФ![]() СаСЊБэЃЌВЂИљОнБэжаЪ§ОнХаЖЯЃЌЪЧЗёга
СаСЊБэЃЌВЂИљОнБэжаЪ§ОнХаЖЯЃЌЪЧЗёга![]() ЕФАбЮеШЯЮЊЁАГЩМЈгыАрМЖгаЙиЯЕЁБЃП
ЕФАбЮеШЯЮЊЁАГЩМЈгыАрМЖгаЙиЯЕЁБЃП
ЃЈ2ЃЉШєМзАргХаубЇЩњжагаФаЩњ6УћЃЌХЎЩњ4УћЃЌЯжДгжаЫцЛњбЁХЩ3УћбЇЩњВЮМгШЋЪаЪ§бЇОКШќЃЌМЧВЮМгОКШќЕФФаЩњШЫЪ§ЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФЗжВМСагыЦкЭћ.
ЕФЗжВМСагыЦкЭћ.
ИНЃК 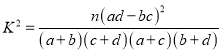
| 0.15 | 0.10 | 0.050 | 0.010 |
| 2.072 | 2.706 | 3.841 | 6.635 |
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com