
【题目】某年级100名学生期中考试数学成绩(单位:分)的频率分布直方图如图所示,其中成绩分组区间是[50,60),[60,70),[70,80),[80,90),[90,100].
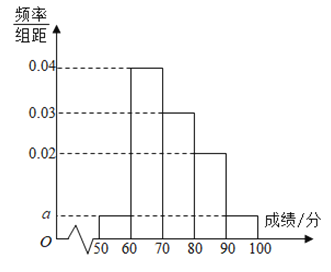
(1)求图中a的值,并根据频率分布直方图估计这100名学生数学成绩的平均分;
(2)从[70,80)和[80,90)分数段内采用分层抽样的方法抽取5名学生,求在这两个分数段各抽取的人数;
(3)现从第(2)问中抽取的5名同学中任选2名参加某项公益活动,求选出的两名同学均来自[70,80)分数段内的概率.
【答案】(1)0.03,73(分)(2)3人和2人(3)P![]()
【解析】
(1)利用频率之和为![]() 列方程,解方程求得
列方程,解方程求得![]() 的值.用每组中点值乘以对应组的频率,然后相加,求得平均分的估计值.
的值.用每组中点值乘以对应组的频率,然后相加,求得平均分的估计值.
(2)根据分层抽样的知识和频率比,求得分别抽取的人数.
(3)利用列举法,结合古典概型概率计算公式,计算出所求概率.
(1)依题意得10×(2×0.005+0.02+a+0.04)=1,解得a=0.03∴这100名学生的数学平均分为: 55×0.05+65×0.4+75×0.3+85×0.2+95×0.05=73(分)
(2)由(1)可知,成绩在[70,80)和[80,90)中的学生人数比为3:2,∴用分层抽样方法抽取成绩在[70,80)和[80,90)中的学生人数分别为3人和2人.
(3)设成绩在[70,80)中的学生为a1,a2,a3,成绩在[80,90)中的学生为b1,b2,则从5人中选取2人的所有结果为:(a1,a2),(a1,a3),(a2,a3),(b1,b2), (a1,b1),(a1,b2),(a2,b1),(a2,b2),(a3,b1),(a3,b2),共10个结果,其中符合条件的共3个结果,∴选出的两名同学均来自[70,80)分数段内的概率为P![]() .
.


科目:高中数学 来源: 题型:
【题目】汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”是我国古代数学的瑰宝.如图所示的弦图中,由四个全等的直角三角形和一个正方形构成.现有五种不同的颜色可供涂色,要求相邻的区域不能用同一种颜色,则不同的涂色方案有( )
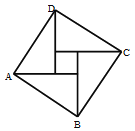
A.180B.192C.420D.480
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列事件:①任取这三条线段,这三条线段恰好组成直角三角形;②从一个三角形的三个顶点各任画一条射线,这三条射线交于一点;③实数![]() ,
,![]() 都不为,但
都不为,但![]() ;④明年12月28日的最高气温高于今年12月28日的最高气温.其中为随机事件的是( )
;④明年12月28日的最高气温高于今年12月28日的最高气温.其中为随机事件的是( )
A.①②③④B.①②④C.①③④D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a∈R,函数f(x)=(-x2+ax)ex(x∈R).
(1)当a=2时,求函数f(x)的单调区间;
(2)若函数f(x)在(-1,1)上单调递增,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一个![]() 的方格表的每个方格内填入1或
的方格表的每个方格内填入1或![]() ,如果任意一格内的数都等于与它有公共边的那些方格内所填数的乘积,则称这种填法是“成功”的.求“成功”填法的总数.
,如果任意一格内的数都等于与它有公共边的那些方格内所填数的乘积,则称这种填法是“成功”的.求“成功”填法的总数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若存在
,若存在![]() ,使
,使![]() 成立, 则称点
成立, 则称点![]() 为函数
为函数![]() 的不动点.
的不动点.
(1)若函数![]() 有不动点
有不动点![]() 和
和![]() , 求
, 求![]() 的值 ;
的值 ;
(2)若对于任意实数![]() ,函数
,函数![]() 总有 2 个相异的不动点 , 求实数
总有 2 个相异的不动点 , 求实数![]() 的取值范围;
的取值范围;
(3)若定义在实数集 R 上的奇函数![]() 存在(有限的)
存在(有限的)![]() 个不动点 , 求证:
个不动点 , 求证:![]() 必为奇数.
必为奇数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校有n个班(n为给定正整数),且每班的男生与女生人数至多相差1.现该学校进行乒乓球比赛,规则如下:同一班的选手之间不比赛,不同班的每两名选手都比赛一场.我们称在同性别选手间的比赛为同打,异性别选手间的比赛为异打.若同打场数与异打场数至多相差1,求有奇数名学生的班级至多有多少个?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com