Question

【题目】已知函数f（x）=（x﹣2）ex+ax（a∈R）
（1）试确定函数f（x）的零点个数；
（2）设x1 ， x2是函数f（x）的两个零点，当x1+x2≤2时，求a的取值范围．

Answer 1

【答案】
（1）解：由f（x）=（x﹣2）ex+ax=0得ax=（2﹣x）ex，

令g（x）=（2﹣x）ex，则g′（x）=﹣ex+（2﹣x）ex=（1﹣x）ex，

∴当x＞1时，g′（x）＜0，当x＜1时，g′（x）＞0，

∴g（x）在（﹣∞，1）上单调递增，在（1，+∞）上单调递减，

∴当x=1时，函数g（x）有最大值g（1）=e，

又当x＜1时，g（x）=（2﹣x）ex＞0，g（2）=0；

作出y=g（x）与y=ax的函数图象如图所示：

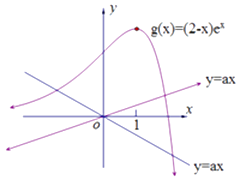
∴当a≥0时，y=ax与g（x）只有一个公共点，从而函数f（x）有一个零点；

当a＜0时，y=ax与g（x）有两个公共点，从而函数f（x）有两个零点．

（2）解：设x1＜x2，由（I）知a＜0且x1＜0，x2＞2，

由f（x1）=（x1﹣2）e +ax1=0，得a= （x1＜0），

由f（x2）=（x2﹣2）e +ax2=0，得a= （x2＞2）．

∴a2= ，

∵x1+x2≤2，∴4﹣2（x1+x2）≥0，0＜e ≤e2，（当且仅当x1+x2=2时取等号）

∴4﹣2（x1+x2）+x1x2≥x1x2，又x1x2＜0，

∴ ≤1，

∴a2≤e ≤e2，

又a＜0，∴﹣e≤a＜0．

【解析】（1）做出y=（2﹣x）ex和y=ax的函数图象，根据函数图象的交点个数判断；（2）分别用x1 ， x2表示出a，得出a2关于x1 ， x2的表达式，利用不等式的性质化简得出a2的范围，从而得出a的范围．