
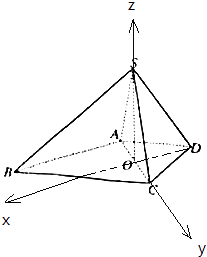
【题目】如图,在底面为梯形的四棱锥S﹣ABCD中,已知AD∥BC,∠ASC=60°,∠BAD=135°,AD=DC= ![]() ,SA=SC=SD=2,O为AC中点.
,SA=SC=SD=2,O为AC中点. 
(1)求证:SO⊥平面ABCD;
(2)求二面角A﹣SB﹣C的余弦值.
【答案】
(1)证明:∵在△ASC中,SA=SC,∠ASC= ![]() ,O为AC中点,
,O为AC中点,
∴△ASC为正三角形,且AC=2,OS= ![]() ,
,
∵在△ADC中,DA2+DC2=4=AC2,O为AC中点,
∴ ![]() ,且OD=1,
,且OD=1,
∵在△SOD中,OS2+OD2=SD2,
∴△SOD为直角三角形,且 ![]() ,
,
∴SO⊥OD,
又∵SO⊥AC,且AC∩OD=O,
∴SO⊥平面ABCD.
(2)解:如图,设直线DO与BC交于点E,则OE、OC、OS两两垂直,
以O为原点,分别以OE,OC,OS所成直线为x,y,z轴,建立空间直角坐标系,
由(1)知∠DAC=45°,且∠BAD=135°,
∴∠BAC=90°,∴AB∥x轴,
又∵在△ABC中,AB=2,
∴A(0,﹣1,0),B(2,﹣1,0),C(0,1,0),S(0,0, ![]() ),
),
![]() =(2,0,0),
=(2,0,0), ![]() =(0,1,
=(0,1, ![]() ),
), ![]() =(2,﹣1,﹣
=(2,﹣1,﹣ ![]() ),
), ![]() =(0,1,﹣
=(0,1,﹣ ![]() ),
),
设平面ABS的一个法向量 ![]() =(x,y,z),
=(x,y,z),
则 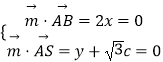 ,令z=﹣1,得
,令z=﹣1,得 ![]() =(0,
=(0, ![]() ,﹣1),|
,﹣1),| ![]() |=2,
|=2,
设平面SBC的法向量 ![]() =(a,b,c),
=(a,b,c),
则 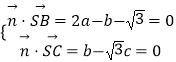 ,取a=
,取a= ![]() ,得
,得 ![]() =(
=( ![]() ),
),
cos< ![]() >=
>= ![]() =
= ![]() =
= ![]() ,
,
∴二面角A﹣SB﹣C的余弦值是 ![]() .
.
【解析】(1)推导出△ASC为正三角形,且AC=2,OS= ![]() ,
, ![]() ,且OD=1,SO⊥OD,由此能证明SO⊥平面ABCD.(2)以O为原点,分别以OE,OC,OS所成直线为x,y,z轴,建立空间直角坐标系,由此能求出二面角A﹣SB﹣C的余弦值.
,且OD=1,SO⊥OD,由此能证明SO⊥平面ABCD.(2)以O为原点,分别以OE,OC,OS所成直线为x,y,z轴,建立空间直角坐标系,由此能求出二面角A﹣SB﹣C的余弦值.
【考点精析】解答此题的关键在于理解直线与平面垂直的判定的相关知识,掌握一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知各项均为正数的数列{an}的首项a1=1,sn是数列{an}的前n项和,且满足:
anSn+1﹣an+1Sn+an﹣an+1=λanan+1(λ≠0,n∈N )
(1)若a1 , a2 , a3成等比数列,求实数λ的值;
(2)若λ= ![]() ,求Sn .
,求Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f (x)=(x+1)lnx﹣a (x﹣1)在x=e处的切线与y轴相交于点(0,2﹣e).
(1)求a的值;
(2)函数f (x)能否在x=1处取得极值?若能取得,求此极值;若不能,请说明理由.
(3)当1<x<2时,试比较 ![]() 与
与 ![]() 大小.
大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点P(3,0)在圆C:(x﹣m)2+(y﹣2)2=40内,动直线AB过点P且交圆C于A、B两点,若△ABC的面积的最大值为20,则实数m的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】太极图是由黑白两个鱼形纹组成的图案,俗称阴阳鱼,太极图展现了一种相互转化,相对统一的和谐美,定义:能够将圆![]() 的周长和面积同时等分成两个部分的函数称为圆
的周长和面积同时等分成两个部分的函数称为圆![]() 的一个“太极函数”,则下列有关说法中:
的一个“太极函数”,则下列有关说法中:

①对于圆![]() 的所有非常数函数的太极函数中,一定不能为偶函数;
的所有非常数函数的太极函数中,一定不能为偶函数;
②函数![]() 是圆
是圆![]() 的一个太极函数;
的一个太极函数;
③存在圆![]() ,使得
,使得![]() 是圆
是圆![]() 的一个太极函数;
的一个太极函数;
④直线![]() 所对应的函数一定是圆
所对应的函数一定是圆![]() 的太极函数;
的太极函数;
⑤若函数![]() 是圆
是圆![]() 的太极函数,则
的太极函数,则![]()
所有正确的是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=|x﹣1|﹣2|x+1|的最大值为m.
(1)求m;
(2)若a,b,c∈(0,+∞),a2+2b2+c2=m,求ab+bc的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=1﹣ax+lnx,(x>0),函数g(x)满足g(x)=x﹣1,(x∈R).
(1)若函数f(x)在x=1时存在极值,求a的值;
(2)在(1)的条件下,当x>1时,blnx< ![]() ,求实数b的取值范围.
,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() cos(2x﹣
cos(2x﹣ ![]() )﹣2sinxcosx.(13分)
)﹣2sinxcosx.(13分)
(Ⅰ)求f(x)的最小正周期;
(Ⅱ)求证:当x∈[﹣ ![]() ,
, ![]() ]时,f(x)≥﹣
]时,f(x)≥﹣ ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com