
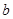 和
和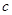 分别是先后抛掷一枚骰子得到的点数,用随机变量
分别是先后抛掷一枚骰子得到的点数,用随机变量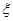 表示方程
表示方程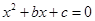 实根的个数(重根按一个计).
实根的个数(重根按一个计).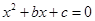 有实根的概率;
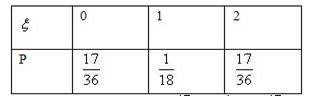
有实根的概率;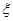 的分布列和数学期望;
的分布列和数学期望;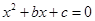 有实根的概率.
有实根的概率.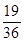
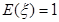

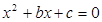 有实根的概率为
有实根的概率为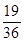
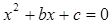 实根的个数得到
实根的个数得到 ,
,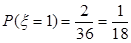 ,
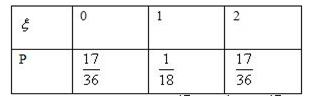
,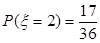 ,
,
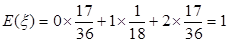
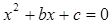 有实根”为事件N,
有实根”为事件N,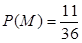 ,
,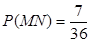 ∴
∴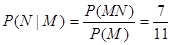


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.3.84 | B.4.84 | C.8.16 | D.9.16 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.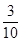 | B. | C.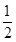 | D.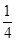 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
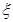 (单位:月)服从正态分布
(单位:月)服从正态分布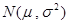 ,且使用寿命不少于
,且使用寿命不少于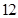 个月的概率为
个月的概率为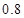 ,使用寿命不少于
,使用寿命不少于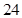 个月的概率为
个月的概率为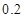 .
.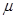 ;
;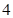 支这种新灯管,使用
支这种新灯管,使用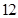 个月时进行一次检查,将已经损坏的灯管换下(中途不更换),求至少两支灯管需要更换的概率.
个月时进行一次检查,将已经损坏的灯管换下(中途不更换),求至少两支灯管需要更换的概率.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.P(A|B)=P(B|A) | B.0<P(B|A)<1 | C.P(AB)=P(A)•P(B|A) | D.P(A∩B|A)=P(B) |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
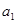 ,按下列方法操作一次产生一个新的实数:由甲、乙同时各抛一枚均匀的硬币,如果出现两个正面朝上或两个反面朝上,则把
,按下列方法操作一次产生一个新的实数:由甲、乙同时各抛一枚均匀的硬币,如果出现两个正面朝上或两个反面朝上,则把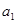 乘以2后再减去12;如果出现一个正面朝上,一个反面朝上,则把
乘以2后再减去12;如果出现一个正面朝上,一个反面朝上,则把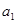 除以2后再加上12,这样就可得到一个新的实数
除以2后再加上12,这样就可得到一个新的实数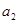 ,对
,对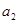 仍按上述方法进行一次操作,又得到一个新的实数
仍按上述方法进行一次操作,又得到一个新的实数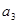 ,当
,当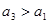 时,甲获胜,否则乙获胜。若甲获胜的概率为
时,甲获胜,否则乙获胜。若甲获胜的概率为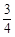 ,则
,则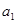 的取值范围是_________.
的取值范围是_________.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com