
【题目】某大学餐饮中心为了了解新生的饮食习惯,在全校一年级学生中进行了抽样调查,调查结果如下表所示:
喜欢甜品 | 不喜欢甜品 | 合计 | |
南方学生 | 60 | 20 | 80 |
北方学生 | 10 | 10 | 20 |
合计 | 70 | 30 | 100 |
![]() 根据表中数据,问是否有
根据表中数据,问是否有![]() 的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
![]() 已知在被调查的北方学生中有5名数学系的学生,其中2名喜欢甜品,现在从这5名学生中随机抽取3人,求至多有1人喜欢甜品的概率.
已知在被调查的北方学生中有5名数学系的学生,其中2名喜欢甜品,现在从这5名学生中随机抽取3人,求至多有1人喜欢甜品的概率.
附:![]()
|
|
|
|
|
|
|
|
|
|
【答案】(1)有![]() %的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;(2)
%的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;(2)![]() .
.
【解析】
(1)将![]() 列联表中的数据,代入公式,求得
列联表中的数据,代入公式,求得![]() 的值,即可做出判断;
的值,即可做出判断;
(2)从![]() 名数学教师中任选
名数学教师中任选![]() 人,列举出所有的基本事件的总数,即可利用古典概型及概率的计算公式求解.
人,列举出所有的基本事件的总数,即可利用古典概型及概率的计算公式求解.
解(1)将2×2列联表中的数据代入公式计算,得
χ2=![]() =
=![]() ≈4.762.
≈4.762.
由于4.762>3.841,所以有95%的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”..
(2)从5名数学系学生中任取3人的一切可能结果所组成的基本事件空间Ω={(a1,a2,b1),(a1,a2,b2),(a1,a2,b3),(a1,b1,b2),(a1,b2,b3),(a1,b1,b3),(a2,b1,b2),(a2,b2,b3),(a2,b1,b3),(b1,b2,b3)}.
其中ai表示喜欢甜品的学生,i=1,2.bj表示不喜欢甜品的学生,j=1,2,3.Ω由10个基本事件组成,且这些基本事件的出现是等可能的..
用A表示“3人中至多有1人喜欢甜品”这一事件,则
A={(a1,b1,b2),(a1,b2,b3),(a1,b1,b3),(a2,b1,b2),(a2,b2,b3),(a2,b1,b3),(b1,b2,b3)}.
事件A是由7个基本事件组成,因而P(A)=![]() ...
...


科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 是异面直线,
是异面直线,![]() 是
是![]() ,
,![]() 外的一点,则下列结论中正确的是( )
外的一点,则下列结论中正确的是( )
A.过![]() 有且只有一条直线与
有且只有一条直线与![]() ,
,![]() 都垂直B.过
都垂直B.过![]() 有且只有一条直线与
有且只有一条直线与![]() ,
,![]() 都平行
都平行
C.过![]() 有且只有一个平面与
有且只有一个平面与![]() ,
,![]() 都垂直D.过
都垂直D.过![]() 有且只有一个平面与
有且只有一个平面与![]() ,
,![]() 都平行
都平行
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=aex图象在x=0处的切线与函数g(x)=lnx图象在x=1处的切线互相平行.
(Ⅰ)求a的值;
(Ⅱ)设直线x=t(t>0)分别与曲线y=f(x)和y=g(x)交于P,Q两点,求证:|PQ|>2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知A(﹣2![]() ,0),B
,0),B![]() ,M(x,y)是曲线C上的动点,且直线AM与BM的斜率之积等于
,M(x,y)是曲线C上的动点,且直线AM与BM的斜率之积等于![]() .
.
(1)求曲线C方程;
(2)过D(2,0)的直线l(l与x轴不垂直)与曲线C交于E,F两点,点F关于x轴的对称点为F′,直线EF′与x轴交于点P,求△PEF的面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() =1(a>0,b>0)的左、右焦点分别为F1,F2,点O为双曲线的中心,点P在双曲线右支上,△PF1F2内切圆的圆心为Q,圆Q与x轴相切于点A,过F2作直线PQ的垂线,垂足为B,则下列结论成立的是( )
=1(a>0,b>0)的左、右焦点分别为F1,F2,点O为双曲线的中心,点P在双曲线右支上,△PF1F2内切圆的圆心为Q,圆Q与x轴相切于点A,过F2作直线PQ的垂线,垂足为B,则下列结论成立的是( )
A. |OA|>|OB|B. |OA|<|OB|
C. |OA|=|OB|D. |OA|与|OB|大小关系不确定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,抛物线关于![]() 轴对称,它的顶点在坐标原点,点
轴对称,它的顶点在坐标原点,点![]() 、
、![]() 、
、![]() 均在抛物线上.
均在抛物线上.
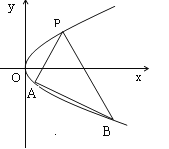
(1)写出该抛物线的方程及其准线方程;
(2)当![]() 与
与![]() 的斜率存在且倾斜角互补时,求
的斜率存在且倾斜角互补时,求![]() 的值及直线
的值及直线![]() 的斜率.
的斜率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com