
设实数 ,整数
,整数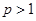 ,
, .
.
(1)证明:当 且
且 时,
时, ;
;
(2)数列 满足
满足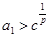 ,
,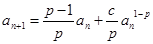 ,证明:
,证明: .
.
(1)证明:当 且
且 时,
时, ;(2)
;(2) .
.
解析试题分析:(1)证明原不等式成立,可以用数学归纳法,当 时,当
时,当 ,由
,由 成立.得出当
成立.得出当 时,
时,
 ,综合以上当
,综合以上当 且
且 时,对一切整数
时,对一切整数 ,不等式
,不等式 均成立.(2)可以有两种方法证明:第一种方法,先用数学归纳法证明
均成立.(2)可以有两种方法证明:第一种方法,先用数学归纳法证明 .其中要利用到当
.其中要利用到当 时,
时, .当
.当 得
得 .由(1)中的结论得
.由(1)中的结论得 .因此
.因此 ,即
,即 .所以
.所以 时,不等式
时,不等式 也成立.综合①②可得,对一切正整数
也成立.综合①②可得,对一切正整数 ,不等式
,不等式 均成立.再证由
均成立.再证由 可得
可得 ,即
,即 .第二种方法,构造函数设
.第二种方法,构造函数设 ,则
,则 ,并且
,并且 .由此可得,
.由此可得, 在
在 上单调递增,因而,当
上单调递增,因而,当 时,
时, .再利用数学归纳法证明
.再利用数学归纳法证明 .
.
(1)证明:用数学归纳法证明
①当 时,
时, ,原不等式成立.
,原不等式成立.
②假设 时,不等式
时,不等式 成立.
成立.
当 时,
时,
所以 时,原不等式也成立.
时,原不等式也成立.
综合①②可得,当 且
且 时,对一切整数
时,对一切整数 ,不等式
,不等式 均成立.
均成立.
证法1:先用数学归纳法证明 .
.
①当 时,由题设
时,由题设 知
知 成立.②假设
成立.②假设 时,不等式
时,不等式 成立.
成立.
由 易知
易知 .
.
当 时,
时, .
.
当 得
得 .
.
由(1)中的结论得 .
.
因此 ,即
,即 .所以
.所以 时,不等式
时,不等式

 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:解答题
某同学在一次研究性学习中发现以下四个不等式都是正确的: ;
; ;
; ;
; .
.
请你观察这四个不等式:
(1)猜想出一个一般性的结论(用字母表示);
(2)证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com