
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() :
:![]() ,直线
,直线![]() :
:![]() .以极点
.以极点![]() 为原点,极轴为
为原点,极轴为![]() 轴的正半轴建立平面直角坐标系.
轴的正半轴建立平面直角坐标系.
(1)求直线![]() ,
,![]() 的直角坐标方程以及曲线
的直角坐标方程以及曲线![]() 的参数方程;
的参数方程;
(2)已知直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,直线
两点,直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的面积.
的面积.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)=-x3+ax2+b(a,b∈R).
(1)当a>0时,若f(x)满足:y极小值=1,y极大值=![]() ,试求f(x)的解析式;
,试求f(x)的解析式;
(2)若x∈[0,1]时,y=f(x)图象上的任意一点处的切线斜率k满足:|k|≤1,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“双十一网购狂欢节”源于淘宝商城(天猫)![]() 年
年![]() 月
月![]() 日举办的促销活动,当时参与的商家数量和促销力度均有限,但营业额远超预想的效果,于是
日举办的促销活动,当时参与的商家数量和促销力度均有限,但营业额远超预想的效果,于是![]() 月
月![]() 日成为天猫举办大规模促销活动的固定日期.如今,中国的“双十一”已经从一个节日变成了全民狂欢的“电商购物日”.某淘宝电商为分析近
日成为天猫举办大规模促销活动的固定日期.如今,中国的“双十一”已经从一个节日变成了全民狂欢的“电商购物日”.某淘宝电商为分析近![]() 年“双十一”期间的宣传费用
年“双十一”期间的宣传费用![]() (单位:万元)和利润
(单位:万元)和利润![]() (单位:十万元)之间的关系,搜集了相关数据,得到下列表格:
(单位:十万元)之间的关系,搜集了相关数据,得到下列表格:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)请用相关系数![]() 说明
说明![]() 与
与![]() 之间是否存在线性相关关系(当
之间是否存在线性相关关系(当![]() 时,说明
时,说明![]() 与
与![]() 之间具有线性相关关系);
之间具有线性相关关系);
(2)建立![]() 关于
关于![]() 的线性回归方程(系数精确到
的线性回归方程(系数精确到![]() ),预测当宣传费用为
),预测当宣传费用为![]() 万元时的利润.
万元时的利润.
附参考公式:回归方程![]() 中
中![]() 和
和![]() 最小二乘估计公式分别为
最小二乘估计公式分别为
 ,
,![]() ,相关系数
,相关系数
参考数据:![]() ,
,![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() (2,1),
(2,1),![]() (1,7),
(1,7),![]() (5,1),设C是直线OP上的一点(其中O为坐标原点)
(5,1),设C是直线OP上的一点(其中O为坐标原点)
(1)求使![]() 取到最小值时的
取到最小值时的![]() ;
;
(2)根据(1)中求出的点C,求cos∠ACB.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某分公司经销某种品牌产品,每件产品的成本为30元,并且每件产品须向总公司缴纳![]() 元(
元(![]() 为常数,
为常数,![]() )的管理费.根据多年的统计经验,预计当每件产品的售价为
)的管理费.根据多年的统计经验,预计当每件产品的售价为![]() 元时,产品一年的销售量为
元时,产品一年的销售量为![]() 为自然对数的底数)万件.已知每件产品的售价为40元时,该产品一年的销售量为500万件.经物价部门核定每件产品的售价
为自然对数的底数)万件.已知每件产品的售价为40元时,该产品一年的销售量为500万件.经物价部门核定每件产品的售价![]() 最低不低于35元,最高不超过41元.
最低不低于35元,最高不超过41元.
(Ⅰ)求分公司经营该产品一年的利润![]() 万元与每件产品的售价
万元与每件产品的售价![]() 元的函数关系式;
元的函数关系式;
(Ⅱ)当每件产品的售价为多少元时,该产品一年的利润![]() 最大,并求
最大,并求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班50名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果按如下方式分成五组:第一组![]() ,第二组
,第二组![]() ,…,第五组
,…,第五组![]() ,下图是按上述分组方法得到的频率分布直方图.
,下图是按上述分组方法得到的频率分布直方图.
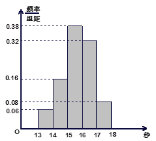
(1)若成绩大于等于14秒且小于16秒为良好,求该班在这次百米测试中成绩良好的人数;
(2)若从第一、五组中随机取出两个成绩,求这两个成绩的差的绝对值大于1的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区工会利用 “健步行APP”开展健步走积分奖励活动.会员每天走5千步可获积分30分(不足5千步不积分),每多走2千步再积20分(不足2千步不积分).为了解会员的健步走情况,工会在某天从系统中随机抽取了1000名会员,统计了当天他们的步数,并将样本数据分为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 九组,整理得到如下频率分布直方图:
九组,整理得到如下频率分布直方图:
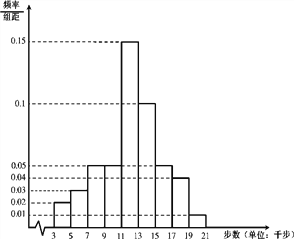
(Ⅰ)求当天这1000名会员中步数少于11千步的人数;
(Ⅱ)从当天步数在![]() ,
, ![]() ,
, ![]() 的会员中按分层抽样的方式抽取6人,再从这6人中随机抽取2人,求这2人积分之和不少于200分的概率;
的会员中按分层抽样的方式抽取6人,再从这6人中随机抽取2人,求这2人积分之和不少于200分的概率;
(Ⅲ)写出该组数据的中位数(只写结果).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com