练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】《九章算术》卷第六《均输》中，提到如下问题：“今有竹九节，下三节容量四升，上四节容量三升．问中间二节欲均容，各多少？”其大致意思是说，若九节竹每节的容量依次成等差数列，下三节容量四升，上四节容量三升，则中间两节的容量各是（　　）

    A.升、升B.升、升

    C.升、升D.升、升

    【答案】D

    【解析】

    由题意知九节竹的容量成等差数列，至下而上各节的容量分别为a1，a2，…，an，公差为d，利用等差数列的前n项和公式和通项公式列出方程组，求出首项和公差，由此能求出中间一节的容量．

    由题意知九节竹的容量成等差数列,

    至下而上各节的容量分别为a1，a2，…，a9，公差为d，

    即=4，=3，

    ∴=4，=3，

    解得,，

    ∴中间两节的容量,，

    故选：D.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，在直三棱柱中，，，，点是的中点.

    （1）求异面直线与所成角的余弦值；

    （2）求平面与所成二面角的正弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系xOy中，曲线C：与直线l：交于M，N两点．

    当时，求的面积的取值范围；

    轴上是否存在点P，使得当k变动时，总有？若存在，求以线段OP为直径的圆的方程；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱柱 中，侧面和侧面都是矩形， 是边长为的正三角形， 分别为的中点.

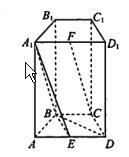
    （1）求证： 平面；

    （2）求证：平面平面.

    （3）若平面，求棱的长度.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，在直四棱柱中，，点是棱上一点.

    （1）求证：平面；

    （2）求证：；

    （3）试确定点的位置，使得平面平面.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若函数恰有两个不同极值点.

    （1）求的取值范围；

    （2）求证：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥P﹣ABCD中，底面ABCD是正方形，E、F分别为PC、BD的中点，侧面PAD⊥底面ABCD．

    （1）求证：EF∥平面PAD；

    （2）若EF⊥PC，求证：平面PAB⊥平面PCD．

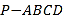
    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】对于区间[a,b](a<b),若函数同时满足：①在[a,b]上是单调函数，②函数在[a,b]的值域是[a,b]，则称区间[a,b]为函数的“保值”区间

    （1）求函数的所有“保值”区间

    （2）函数是否存在“保值”区间？若存在，求的取值范围，若不存在，说明理由

    查看答案和解析>>

    科目：高中数学 来源： 题型：

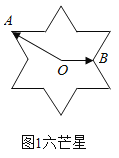
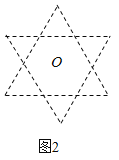
    【题目】如图，“六芒星”是由两个全等正三角形组成，中心重合于点且三组对边分别平行，点是“六芒星”（如图）的两个顶点，动点在“六芒星”上（内部以及边界），若，则的取值可能是（ ）

    A.B.1C.5D.9

    查看答案和解析>>

    同步练习册答案