
【题目】已知函数![]() .
.
(1)若![]() ,求函数
,求函数![]() 的最大值;
的最大值;
(2)令![]() ,讨论函数
,讨论函数![]() 的单调区间;
的单调区间;
(3)若![]() ,正实数
,正实数![]() 满足
满足![]() ,证明
,证明![]() .
.
【答案】(1)f(x)的最大值为f(1)=0.(2)见解析(3)见解析
【解析】
试题(Ⅰ)代入求出![]() 值,利用导数求出函数的极值,进而判断最值;(Ⅱ)求出
值,利用导数求出函数的极值,进而判断最值;(Ⅱ)求出![]() ,求出导函数,分别对参数
,求出导函数,分别对参数![]() 分类讨论,确定导函数的正负,得出函数的单调性;(Ⅲ)整理方程
分类讨论,确定导函数的正负,得出函数的单调性;(Ⅲ)整理方程![]() ,观察题的特点,变形得
,观察题的特点,变形得![]() ,故只需求解右式的范围即可,利用构造函数,求导的方法求出右式的最小值.
,故只需求解右式的范围即可,利用构造函数,求导的方法求出右式的最小值.
试题解析:(Ⅰ)因为![]() ,所以a=-2,此时f(x)=lnx-x2+x,
,所以a=-2,此时f(x)=lnx-x2+x,
f'(x)=![]() -2x+1,
-2x+1,
由f'(x)=0,得x=1,
∴f(x)在(0,1)上单调递增,在(1,+∞)上单调递减,
故当x=1时函数有极大值,也是最大值,所以f(x)的最大值为f(1)=0.
(Ⅱ)g(x)=f(x)-ax2-ax+1,
∴g(x)=lnx-![]() ax2-ax+x+1
ax2-ax+x+1 ![]() ,
,
当a=0时,g'(x)>0,g(x)单调递增;
当a>0时,x∈(0,![]() )时,g'(x)>0,g(x)单调递增;x∈(
)时,g'(x)>0,g(x)单调递增;x∈(![]() ,+∞)时,g'(x)<0,g(x)单调递减;
,+∞)时,g'(x)<0,g(x)单调递减;
当a<0时,g'(x)>0,g(x)单调递增;
(Ⅲ)当a=2时,f(x)=lnx+x2+x,x>0,.
由f(x1)+f(x2)+x1x2=0,即
lnx1+x12+x1+lnx2+x22+x2+x2x1=0.
从而(x1+x2)2+(x1+x2)=x1x2-ln(x1x2),.
令t=x2x1,则由φ(t)=t-lnt得,φ'(t)=![]() .
.
可知,φ(t)在区间(0,1)上单调递减,在区间(1,+∞)上单调递增.所以φ(t)≥1,
所以(x1+x2)2+(x1+x2)≥1,正实数x1,x2,
∴![]() .
.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:高中数学 来源: 题型:
【题目】在直角梯形PBCD中, ![]() ,A为PD的中点,如下左图。将
,A为PD的中点,如下左图。将![]() 沿AB折到
沿AB折到![]() 的位置,使
的位置,使![]() ,点E在SD上,且
,点E在SD上,且![]() ,如下图。
,如下图。
(1)求证: ![]() 平面ABCD;
平面ABCD;
(2)求二面角E—AC—D的正切值.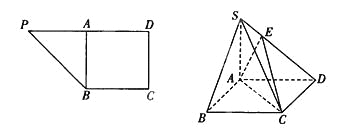
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某面包店随机收集了面包种类的有关数据,经分类整理得到下表:
面包类型 | 第一类 | 第二类 | 第三类 | 第四类 | 第五类 | 第六类 |
面包个数 | 90 | 60 | 30 | 80 | 100 | 40 |
好评率 | 0.6 | 0.45 | 0.7 | 0.35 | 0.6 | 0.5 |
好评率是指:一类面包中获得好评的个数与该类面包的个数的比值.
(1)从面包店收集的面包中随机选取1个,求这个面包是获得好评的第五类面包的概率;
(2)从面包店收集的面包中随机选取1个,估计这个面包没有获得好评的概率;
(3)面包店为增加利润,拟改变生产策略,这将导致不同类型面包的好评率发生变化.假设表格中只有两类面包的好评率数据发生变化,那么哪类面包的好评率增加0.1,哪类面包的好评率减少0.1,使得获得好评的面包总数与样本中的面包总数的比值达到最大?(只需写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某科研团队对某一生物生长规律进行研究,发现其生长蔓延的速度越来越快.开始在某水域投放一定面积的该生物,经过2个月其覆盖面积为18平方米,经过3个月其覆盖面积达到27平方米.该生物覆盖面积![]() (单位:平方米)与经过时间
(单位:平方米)与经过时间![]() 个月的关系有两个函数模型
个月的关系有两个函数模型![]() 与
与![]() 可供选择.
可供选择.
(1)试判断哪个函数模型更合适,并求出该模型的函数解析式;
(2)问约经过几个月,该水域中此生物的面积是当初投放的1000倍![]() (参考数据:
(参考数据:![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 与直线
与直线![]() 相切于点
相切于点![]() ,圆心
,圆心![]() 在
在![]() 轴上.
轴上.
(1)求圆![]() 的方程;
的方程;
(2)过点![]() 且不与
且不与![]() 轴重合的直线
轴重合的直线![]() 与圆
与圆![]() 相交于
相交于![]() 两点,
两点,![]() 为坐标原点,直线
为坐标原点,直线![]() 分别与直线
分别与直线![]() 相交于
相交于![]() 两点,记
两点,记![]() ,
,![]() 的面积分别是
的面积分别是![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
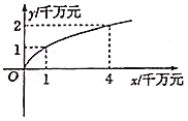
【题目】美国对中国芯片的技术封锁,这却激发了中国“芯”的研究热潮,中国华为公司研发的![]() 、
、![]() 两种芯片都已获得成功.该公司研发芯片已经耗费资金
两种芯片都已获得成功.该公司研发芯片已经耗费资金![]() 千万元,现在准备投入资金进行生产,经市场调查与预测,生产
千万元,现在准备投入资金进行生产,经市场调查与预测,生产![]() 芯片的毛收入与投入的资金成正比,已知每投入
芯片的毛收入与投入的资金成正比,已知每投入![]() 千万元,公司获得毛收入
千万元,公司获得毛收入![]() 千万元;生产
千万元;生产![]() 芯片的毛收入
芯片的毛收入![]() (千万元)与投入的资金
(千万元)与投入的资金![]() (千万元)的函数关系为
(千万元)的函数关系为![]() (
(![]() 与
与![]() 都为常数),其图象如图所示.
都为常数),其图象如图所示.
(1)试分别求出生产![]() 、
、![]() 两种芯片的毛收入
两种芯片的毛收入![]() (千万元)与投入资金
(千万元)与投入资金![]() (千万元)函数关系式;
(千万元)函数关系式;
(2)现在公司准备投入![]() 亿元资金同时生产
亿元资金同时生产![]() 、
、![]() 两种芯片,设投入
两种芯片,设投入![]() 千万元生产
千万元生产![]() 芯片,用
芯片,用![]() 表示公司所获利润,当
表示公司所获利润,当![]() 为多少时,可以获得最大利润?并求最大利润.(利润
为多少时,可以获得最大利润?并求最大利润.(利润![]() 芯片毛收入
芯片毛收入![]() 芯片毛收入
芯片毛收入![]() 研发耗费资金)
研发耗费资金)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com