
����Ŀ��ij�ܹ�˾��A��B���طֱ��мס�������������˾ͬ������Դ��Ʒ����������˾ÿ�춼�̶�����50����Ʒ�����������IJ�Ʒ���ڱ�������.��Ʒ�����г�֮ǰ��Ҫ�Բ�Ʒ�������ܼ�⣬�÷ֵ���80�ֵĶ�Ϊ��Ʒ����Ҫ�����ټӹ����÷ֲ�����80�ֵĶ�Ϊ��Ʒ�����Խ����г�.���Աͳ���˼ס�������������˾100������������ÿ����Ʒӯ��������������������ʾ��
��1
��˾ | �÷� | [50��60�� | [60��70�� | [70��80�� | [80��90�� | [90��100] |
���� | 10 | 10 | 40 | 40 | 50 | |
���� | 10 | 10 | 10 | 10 | 80 |
��2
��˾ | �÷� | [50��60�� | [60��70�� | [70��80�� | [80��90�� | [90��100] |
���� | 10 | 5 | 40 | 45 | 50 | |
���� | 20 | 10 | 20 | 10 | 70 |
��3
ÿ����Ʒ | ÿ����Ʒ | |
��˾ | ӯ2��Ԫ | ��3��Ԫ |
�ҹ�˾ | ӯ3��Ԫ | ��3.5��Ԫ |
��1���ֱ���ס���������˾��100�������IJ�Ʒ����Ʒ�ʣ��ðٷ�����ʾ��.
��2�����ʼס���������˾��100�������IJ�Ʒ���������ĸ�����˵������.
��3�����Լ�˾��100����ÿ���Ʒ�����ܺͶ�Ӧ��Ƶ����Ϊ���ʣ��Ӽ�˾��100�������ȡ1�죬�������Ʒ�����ܺ�ΪX����X�ķֲ��м�����ѧ����.
���𰸡���1����˾��100�������IJ�Ʒ����Ʒ��Ϊ��88%���ҹ�˾��100�������IJ�Ʒ������Ϊ��79%����2���ҹ�˾��100�������IJ�Ʒ����������������������3���ֲ��м���⣬��ѧ����Ϊ![]() ��Ԫ.
��Ԫ.
��������
��1��������Ʒ�����Ʒ�����ı�ֵ���ɣ�
��2���ֱ�������Ƚϼ��ɣ�
��3������X����λ����Ԫ���Ŀ���ȡֵΪ100��50����150�ĸ��ʣ��������Ķ���ɵô�.
��1����˾��100�������IJ�Ʒ����Ʒ��Ϊ��![]() 88%��
88%��
�ҹ�˾��100�������IJ�Ʒ������Ϊ��![]() 79%.
79%.
��2���ҹ�˾��100�������IJ�Ʒ�����������
�������£�
��˾��100�������IJ�Ʒ��������Ϊ��50��80+40��10����2+��50��100��50��80��40��10��������3����7000����Ԫ����
�ҹ�˾��100�������IJ�Ʒ��������Ϊ��50��70+45��10����3+��50��100��50��70��45��10��������3.5����8175����Ԫ����
��Ϊ7000��8175�������ҹ�˾��100�������IJ�Ʒ�����������
��3��X����λ����Ԫ���Ŀ���ȡֵΪ100��50����150��
P��X��100��![]() 0.8.
0.8.
P��X��50��![]() 0.1��
0.1��
P��X��150��![]() 0.1��
0.1��
��X�ķֲ���Ϊ
X | 100 | 50 | ��150 |
P | 0.8 | 0.1 | 0.1 |
��EX��100��0.8+50��0.1+����150����0.1��70����Ԫ����


 ÿ��10���ӿ�����������������ϵ�д�
ÿ��10���ӿ�����������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ȫ�ȼٴ�����Ȫ��![]() ΪԲ�Ľ���һ���뾶Ϊ
ΪԲ�Ľ���һ���뾶Ϊ![]() ��Բ����Ȫ�أ���ͼ��ʾ��
��Բ����Ȫ�أ���ͼ��ʾ��![]() ��
��![]() ��Բ
��Բ![]() �Ϲ���ֱ��
�Ϲ���ֱ��![]() �ԳƵ����㣬��
�ԳƵ����㣬��![]() ΪԲ�ģ�
ΪԲ�ģ�![]() Ϊ�뾶��Բ��Բ
Ϊ�뾶��Բ��Բ![]() ����
����![]() ��
��![]() �ֱ��ڵ�
�ֱ��ڵ�![]() ��
��![]() �������ı���
�������ı���![]() Ϊ��Ȫ����I��II����Ϊ������Ϣ����III��IV����Ϊ������Ϣ������
Ϊ��Ȫ����I��II����Ϊ������Ϣ����III��IV����Ϊ������Ϣ������![]() ��
��
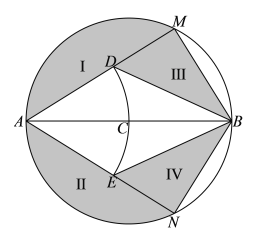
��1����![]() ʱ���������Ϣ�����������III��IV������������ĺͣ���
ʱ���������Ϣ�����������III��IV������������ĺͣ���
��2����������Ϣ������������ʱ����![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����С�����˸��������ʵؾ��ȵ���������Ϸ���������£��������ĵ���֮��Ϊ4�ı���������ԭͶ���˼���Ͷ�����������ĵ���֮�Ͳ���4�ı��������ɶԷ�����Ͷ�����涨��һ�δ�С����ʼ��
��1����ǰ4��Ͷ����С��ǡ��Ͷ��2�εĸ��ʣ�
��2������Ϸ��ǰ4���У�С��Ͷ���Ĵ���Ϊ![]() �����������
�����������![]() �ķֲ�����������
�ķֲ�����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڷ���ij���������¼��ڼ䣬��רҵ������Ϊ���¼���һ��ʱ����û�з������ģȺ���Ⱦ�ı�־��������10�գ�ÿ���������Ʋ���������7����.��֪��ȥ10�գ�![]() ��
��![]() ��
��![]() �����������Ʋ���������Ϣ���£�
�����������Ʋ���������Ϣ���£�
![]() �أ�����ƽ����Ϊ3����λ��Ϊ4��
�أ�����ƽ����Ϊ3����λ��Ϊ4��
![]() �أ�����ƽ����Ϊ2�����巽��Ϊ3��
�أ�����ƽ����Ϊ2�����巽��Ϊ3��
![]() �أ�����ƽ����Ϊ1�����巽�����0��
�أ�����ƽ����Ϊ1�����巽�����0��
��![]() ��
��![]() ��
��![]() �����У�һ��û�з������ģȺ���Ⱦ����__________��.
�����У�һ��û�з������ģȺ���Ⱦ����__________��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����ȷ���ǣ� ��
A.��������![]() ����
����![]() ���ķ�����������
���ķ�����������![]() ����
����![]() ��
��
B.����������ABC�У���A��B����sinA��sinB����������Ϊ������.
C.��![]() ������
������![]() ���ı�Ҫ���������
���ı�Ҫ���������
D.����p��q��Ϊ�����⣬��p��q������һ��Ϊ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() Ϊ��Բ
Ϊ��Բ![]() �ϵ�һ�㣬FΪ��Բ���ҽ��㣬��
�ϵ�һ�㣬FΪ��Բ���ҽ��㣬��![]() ��ֱ��x�ᣬ����ԭ��O��ֱ��
��ֱ��x�ᣬ����ԭ��O��ֱ��![]() ����Բ��A��B���㣬�߶�
����Բ��A��B���㣬�߶�![]() ���е�M��ֱ��
���е�M��ֱ��![]() ��.
��.
��1������ԲC�ı����̣�
��2����![]() ��������ʱ����ֱ��
��������ʱ����ֱ��![]() �ķ���.
�ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ƽ��ֱ������ϵ![]() �У�����
�У�����![]() �IJ�������Ϊ
�IJ�������Ϊ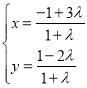 ��
��![]() ��������
Ϊ��������![]() ��.������ԭ��OΪ���㣬x���������Ϊ���Ὠ��������ϵ������
��.������ԭ��OΪ���㣬x���������Ϊ���Ὠ��������ϵ������![]() �ļ����귽��Ϊ
�ļ����귽��Ϊ![]() .
.
��1��������![]() ����ͨ���̺�����
����ͨ���̺�����![]() ��ֱ�����귽�̣�
��ֱ�����귽�̣�
��2����֪��P�ļ�����Ϊ![]() ��QΪ����
��QΪ����![]() �ϵĶ��㣬��
�ϵĶ��㣬��![]() ���е�M������
���е�M������![]() �ľ�������ֵ.
�ľ�������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ϵ��ԭ��OΪ���㣬x��ķǸ�����Ϊ���ᣬ����������ϵ��������������ϵ��ȡ��ͬ�ij��ȵ�λ.��֪Բ![]() ��Բ
��Բ![]() �ļ����귽�̷ֱ���
�ļ����귽�̷ֱ���![]() ��
��![]() .
.
��1����Բ![]() ��Բ
��Բ![]() �Ĺ���������ֱ�ߵ�ֱ�����귽�̣�
�Ĺ���������ֱ�ߵ�ֱ�����귽�̣�
��2��������![]() ��
��![]() ��Բ
��Բ![]() �Ľ���ΪO��P����Բ
�Ľ���ΪO��P����Բ![]() �Ľ���ΪO��Q����
�Ľ���ΪO��Q����![]() �����ֵ.
�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���ϳ�����![]() �������ϣ�����1Ͱ
�������ϣ�����1Ͱ![]() ���ϣ�����ز�ԭ��100�����ʱ��3Сʱ������1Ͱ
���ϣ�����ز�ԭ��100�����ʱ��3Сʱ������1Ͱ![]() ��������ز�ԭ��100�����ʱ��1Сʱ��ÿ��
��������ز�ԭ��100�����ʱ��1Сʱ��ÿ��![]() ���ϵIJ���������
���ϵIJ���������![]() ���ϲ�����2����ÿ��������������������ز�ԭ�ϵ���������750���ÿ������
���ϲ�����2����ÿ��������������������ز�ԭ�ϵ���������750���ÿ������![]() ���ϵ�ʱ�䲻��������
���ϵ�ʱ�䲻��������![]() ���ϵ�ʱ�䣬ÿͰ
���ϵ�ʱ�䣬ÿͰ![]() ���ϵ�������ÿͰ
���ϵ�������ÿͰ![]() ���������1.5�����������ϳ�ÿ������
���������1.5�����������ϳ�ÿ������![]() ����
����![]() Ͱ��
Ͱ��![]() ����
����![]() Ͱʱ��
Ͱʱ��![]() �����������
�����������![]() _____��
_____��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com