【题目】命题“若△ABC的三个内角构成等差数列，则△ABC必有一内角为
”的否命题( )
A.与原命题真假相异B.与原命题真假相同
C.与原命题的逆否命题的真假不同D.与原命题的逆命题真假相异
【答案】B
【解析】
根据命题的否命题与原命题的关系，写出否命题，再根据互为逆否命题的两命题同真假，否命题与逆命题互为逆否命题，则研究原命题的逆命题的真假即可.
解：原命题为：“若
的三内角构成等差数列，则必有一内角为
”，
若
，
，
成等差数列，则
，又
，解得
，所以它是真命题．
否命题为：“若△ABC的三个内角不能构成等差数列，则△ABC中任意内角均不为”
根据互为逆否命题的两命题同真假，否命题与逆命题互为逆否命题，则研究原命题的逆命题的真假，
逆命题为：“若有一内角为，则的三内角构成等差数列”
若有一内角为，不妨设，则
，所以，即的三内角成等差数列，所以逆命题为真，则否命题为真．
所以否命题与原命题同为真命题．
故选：．
科目：高中数学 来源： 题型：
【题目】数学老师给出一个函数
，甲、乙、丙、丁四个同学各说出了这个函数的一条性质：甲：在
上函数单调递减；乙：在
上函数单调递增；丙：在定义域R上函数的图象关于直线
对称；丁：
不是函数的最小值．老师说：你们四个同学中恰好有三个人说的正确．那么，你认为____说的是错误的．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某学校将甲、乙等6名新招聘的老师分配到4个不同的年级，每个年级至少分配1名教师，且甲、乙两名老师必须分到同一个年级，则不同的分法种数为______
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在极坐标系中，圆C的圆心坐标为（1，0），半径为1.
（1）求圆C的极坐标方程；
（2）若以极点O为原点，极轴所在直线为x轴建立平面直角坐标系.已知直线l的参数方程为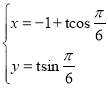
（t为参数），试判断直线l与圆C的位置关系.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】中央电视台为了解一档诗歌类节目的收视情况，抽查东西两部各5个城市，得到观看该节目的人数（单位：千人）如下茎叶图所示：
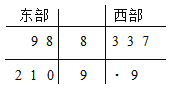
其中一个数字被污损；
（1）求东部各城市观看该节目观众平均人数超过西部各城市观看该节目观众平均人数的概率；
（2）随着节目的播出，极大激发了观众对诗歌知识的学习积累热情，从中获益匪浅.现从观看该节目的观众中随机统计了4位观众的周均学习诗歌知识的时间（单位：小时）与年龄（单位：岁），并制作了对照表（如下表所示）：
由表中数据，试求线性回归方程
，并预测年龄在60岁的观众周均学习诗歌知识的时间.
参考公式：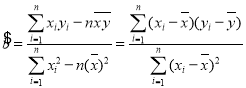
, 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某公司有
四辆汽车，其中
车的车牌尾号为0，
两辆车的车牌尾号为6，
车的车牌尾号为5，已知在非限行日，每辆车都有可能出车或不出车.已知
两辆汽车每天出车的概率为
，两辆汽车每天出车的概率为
，且四辆汽车是否出车是相互独立的.
该公司所在地区汽车限行规定如下：
（1）求该公司在星期四至少有2辆汽车出车的概率；
（2）设
表示该公司在星期一和星期二两天出车的车辆数之和，求的分布列和数学期望.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】随着社会发展对环保的要求，越来越多的燃油汽车被电动汽车取代，为了了解某品牌的电动汽车的节能情况，对某一辆电动汽车“行车数据”的两次记录如下表：
记录时间 | 累计里程 （单位：公里） | 平均耗电量（单位： | 剩余续航里程 （单位：公里） |
2020年1月1日 | 5000 | 0.125 | 380 |
2020年1月2日 | 5100 | 0.126 | 246 |
（注：累计里程指汽车从出厂开始累计行驶的路程，累计耗电量指汽车从出厂开始累计消耗的电量，
）
下面对该车在两次记录时间段内行驶100公里的耗电量估计正确的是（ ）
A.等于
B.到
之间C.等于D.大于
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
