
(1)ЧѓmЕФШЁжЕЗЖЮЇ,ВЂжИГіЕБmБфЛЏЪБЕуBЕФЙьМЃG.
(2)ЙьМЃGЩЯЪЧЗёДцдквЛЕуD,ЫќдкжБЯпy=![]() xЩЯЕФЩфгАЮЊP,ЪЙЕУ
xЩЯЕФЩфгАЮЊP,ЪЙЕУ![]() ЁЄ
ЁЄ![]() =
=![]() ЁЄ
ЁЄ![]() ?ШєДцдк,ЪджИГіЫЋЧњЯпEЕФгвНЙЕуFЗжЯђСП
?ШєДцдк,ЪджИГіЫЋЧњЯпEЕФгвНЙЕуFЗжЯђСП![]() ЫљГЩЕФБШЃЛШєВЛДцдк,ЧыЫЕУїРэгЩ.
ЫљГЩЕФБШЃЛШєВЛДцдк,ЧыЫЕУїРэгЩ.
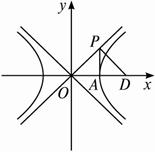
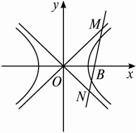
(3)ЕБmЮЊЖЈжЕЪБ,Й§ЙьМЃGЩЯЕФЕуB(m,0)зївЛЬѕжБЯпlгыЫЋЧњЯпEЕФгвжЇНЛгкВЛЭЌЕФСНЕу,ЧвгыжБЯпy=![]() x,y=-
x,y=-![]() xЗжБ№НЛгкM,NСНЕу,ЧѓЁїMONжмГЄЕФзюаЁжЕ.
xЗжБ№НЛгкM,NСНЕу,ЧѓЁїMONжмГЄЕФзюаЁжЕ.
Нт:(1)ЩшM(x,y),дђxЁн3Чвy2=![]() x2-16,
x2-16,
ФЧУДЕуMЕНЕуBЕФОрРыd=![]() =
= .?
.?
Щшf(x)=d2,дђf(x)=![]() (x-
(x-![]() )2+
)2+![]() M2-16(xЁн3). ?
M2-16(xЁн3). ?
ЕБ![]() Ём3МДMЁм
Ём3МДMЁм![]() ЪБ,f(x)ЪЧЃл3,+Ёо)ЩЯЕФдіКЏЪ§,ЫљвдЕБx=3ЪБ,f(x)ШЁзюаЁжЕM-3=|AB|;
ЪБ,f(x)ЪЧЃл3,+Ёо)ЩЯЕФдіКЏЪ§,ЫљвдЕБx=3ЪБ,f(x)ШЁзюаЁжЕM-3=|AB|;
ЕБ![]() ЃО3МДMЃО
ЃО3МДMЃО![]() ЪБ,f(
ЪБ,f(![]() )=
)=![]()
![]() ЃМm-3. ?
ЃМm-3. ?
гЩЩЯЪіПЩЕУ,ЕБЧвНіЕБ3ЁмMЁм![]() ЪБ,MЕНBЕФОрРыЮЊ|AB|.?
ЪБ,MЕНBЕФОрРыЮЊ|AB|.?
ЫљвдЕуBЕФЙьМЃЪЧвЛЬѕЯпЖЮAN,ЦфжаN(![]() ,0),МДЙьМЃGЮЊЯпЖЮAN. ?
,0),МДЙьМЃGЮЊЯпЖЮAN. ?
(2)ЩшДцдкD,СюP(3T,4T),дђD(![]() T,0),?
T,0),?
гкЪЧ![]() =(3T-3,4T),
=(3T-3,4T), ![]() =(
=(![]() T,0),?
T,0),?
Ёр![]() ЁЄ
ЁЄ![]() =25T2-25T.?
=25T2-25T.?
гж![]() ЁЄ
ЁЄ![]() =0, Ёр25T2-25T=0.?
=0, Ёр25T2-25T=0.?
ЁрT=0ЛђT=1. ?
ЕБT=0ЪБ,DЮЊ(0,0)ВЛТњзуЬтвт;?
ЕБT=1ЪБ,DЮЊ(![]() ,0)дкЙьМЃGЩЯ,?
,0)дкЙьМЃGЩЯ,?
ЁрДцдкDТњзуЬтвт.ДЫЪБD(![]() ,0),F(5,0),?
,0),F(5,0),?
га![]() =(2,0),
=(2,0),![]() =(
=(![]() ,0),
,0),![]() =
=![]()
![]() .?
.?
ДгЖјFЗж![]() ЫљГЩЕФБШЮЊІЫ=
ЫљГЩЕФБШЮЊІЫ=![]() . ?
. ?
(3)ЩшM(3s,4s),N(3T,-4T),?
вђЮЊжБЯпlгыЫЋЧњЯпEЕФгвжЇгаСНИіНЛЕу,ЫљвдsЃО0,TЃО0.?
гЩM,B,NЙВЯпжЊ![]() =
=![]() ,МД
,МД![]() =
=![]() . ?
. ?
Жј![]() (s+T)=(
(s+T)=(![]() )(s+T)=2+
)(s+T)=2+![]() Ён2+2
Ён2+2![]() =4.?
=4.?
Ыљвдs+TЁн![]() ,ЕБЧвНіЕБs=T=
,ЕБЧвНіЕБs=T=![]() ЪБШЁЕШКХ. ?
ЪБШЁЕШКХ. ?
ЁїOMNЕФжмГЄL=|OM|+|ON|+|MN|=5s+5T+![]() ?
?
=5(s+T)+![]() ?
?
Ён9(s+T)Ён
Ыљвд,ЕБs=T=![]() ЪБ,ЁїOMNЕФжмГЄзюаЁЮЊ
ЪБ,ЁїOMNЕФжмГЄзюаЁЮЊ


 ЦкФЉ100ЗжДГЙиКЃЕэПМЭѕЯЕСаД№АИ
ЦкФЉ100ЗжДГЙиКЃЕэПМЭѕЯЕСаД№АИ аЁбЇФмСІВтЪдОэЯЕСаД№АИ
аЁбЇФмСІВтЪдОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
вбжЊНЙЕудкxжсЩЯЕФЫЋЧњЯпCЕФСНЬѕНЅНќЯпЙ§зјБъдЕуЃЌЧвСНЬѕНЅНќЯпгывдЕуA (0ЃЌ![]() )ЮЊдВаФЃЌ1ЮЊАыОЖЕФдВЯрЧаЃЌгжжЊCЕФвЛИіНЙЕугыAЙигкy = xЖдГЦЃЎ
)ЮЊдВаФЃЌ1ЮЊАыОЖЕФдВЯрЧаЃЌгжжЊCЕФвЛИіНЙЕугыAЙигкy = xЖдГЦЃЎ
ЃЈ1ЃЉЧѓЫЋЧњЯпCЕФЗНГЬЃЛ
ЃЈ2ЃЉШєQЪЧЫЋЧњЯпЯпCЩЯЕФШЮвЛЕуЃЌF1ЃЌF2ЮЊЫЋЧњЯпCЕФзѓЁЂгвСНИіНЙЕуЃЌДгF1в§ЁЯF1QF2ЕФЦНЗжЯпЕФДЙЯпЃЌДЙзуЮЊNЃЌЪдЧѓЕуNЕФЙьМЃЗНГЬЃЛ
ЃЈ3ЃЉЩшжБЯпy = mx + 1гыЫЋЧњЯпCЕФзѓжЇНЛгкAЁЂBСНЕуЃЌСэвЛжБЯпlОЙ§M (ЈC2ЃЌ0)МАABЕФжаЕуЃЌЧѓжБЯпlдкyжсЩЯЕФНиОрbЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com