
【题目】如图,已知点![]() 在圆柱
在圆柱![]() 的底面
的底面![]() 上,
上,![]() ,
,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的直径,且
的直径,且![]() .若圆柱
.若圆柱![]() 的体积
的体积![]() ,
,![]() ,
,![]() ,回答下列问题:
,回答下列问题:
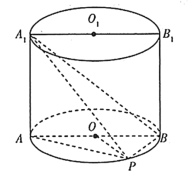
(1)求三棱锥![]() 的体积.
的体积.
(2)在线段AP上是否存在一点M,使异面直线OM与![]() 所成的角的余弦值为
所成的角的余弦值为![]() ?若存在,请指出点M的位置,并证明;若不存在,请说明理由.
?若存在,请指出点M的位置,并证明;若不存在,请说明理由.
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知抛物线
中,已知抛物线![]() :
:![]() ,过抛物线焦点
,过抛物线焦点![]() 且与
且与![]() 轴垂直的直线与抛物线相交于
轴垂直的直线与抛物线相交于![]() 、
、![]() 两点,且
两点,且![]() 的周长为
的周长为![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)若直线![]() 过焦点
过焦点![]() 且与抛物线
且与抛物线![]() 相交于
相交于![]() 、
、![]() 两点,过点
两点,过点![]() 、
、![]() 分别作抛物线
分别作抛物线![]() 的切线
的切线![]() 、
、![]() ,切线
,切线![]() 与
与![]() 相交于点
相交于点![]() ,求:
,求:![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电子科技公司由于产品采用最新技术,销售额不断增长,最近![]() 个季度的销售额数据统计如下表(其中
个季度的销售额数据统计如下表(其中![]() 表示
表示![]() 年第一季度,以此类推):
年第一季度,以此类推):
季度 |
|
|
|
|
|
季度编号x |
|
|
|
|
|
销售额y(百万元) |
|
|
|
|
|
(1)公司市场部从中任选![]() 个季度的数据进行对比分析,求这
个季度的数据进行对比分析,求这![]() 个季度的销售额都超过
个季度的销售额都超过![]() 千万元的概率;
千万元的概率;
(2)求![]() 关于
关于![]() 的线性回归方程,并预测该公司
的线性回归方程,并预测该公司![]() 的销售额.
的销售额.
附:线性回归方程:![]() 其中
其中 ,
,![]()
参考数据:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中央政府为了应对因人口老龄化而造成的劳动力短缺等问题,拟定出台“延迟退休年龄政策”.为了了解人们对“延迟退休年龄政策”的态度,责成人社部进行调研.人社部从网上年龄在15~65岁的人群中随机调查100人,调查数据的频率分布直方图如图所示, 支持“延迟退休年龄政策”的人数与年龄的统计结果如表:

年龄(岁) |
|
|
|
|
|
支持“延迟退休年龄政策”人数 | 15 | 5 | 15 | 28 | 17 |
(I)由以上统计数据填写下面的![]() 列联表;
列联表;
年龄低于45岁的人数 | 年龄不低于45岁的人数 | 总计 | |
支持 | |||
不支持 | |||
总计 |
(II)通过计算判断是否有![]() 的把握认为以45岁为分界点的不同人群对“延迟退休年龄政策”的态度有差异.
的把握认为以45岁为分界点的不同人群对“延迟退休年龄政策”的态度有差异.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
参考公式:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某专卖店为了对新产品进行合理定价,将该产品按不同的单价试销,调查统计如下表:
售价 | 4 | 5 | 6 | 7 | 8 |
周销量 | 90 | 85 | 83 | 79 | 73 |
(1)求周销量y(件)关于售价x(元)的线性回归方程![]() ;
;
(2)按(1)中的线性关系,已知该产品的成本为2元/件,为了确保周利润大于598元,则该店应该将产品的售价![]() 定为多少?
定为多少?
参考公式: ,
,![]() .
.
参考数据:![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小型企业甲产品生产的投入成本x(单位:万元)与产品销售收入y(单位:万元)存在较好的线性关系,下表记录了最近5次该产品的相关数据.
x(万元) | 3 | 5 | 7 | 9 | 11 |
y(万元) | 8 | 10 | 13 | 17 | 22 |
(1)求y关于x的线性回归方程;
(2)根据(1)中的回归方程,判断该企业甲产品投入成本12万元的毛利率更大还是投入成本15万元的毛利率更大(毛利率![]()
![]()
![]() )?
)?
相关公式: ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体![]() 的棱长为
的棱长为![]() ,
, ![]() 分别是
分别是![]() 的中点,点
的中点,点![]() 在棱
在棱![]()
上, ![]() (
(![]() ).
).

(Ⅰ)三棱锥![]() 的体积分别为
的体积分别为![]() ,当
,当![]() 为何值时,
为何值时, ![]() 最大?最大值为多少?
最大?最大值为多少?
(Ⅱ)若![]() 平面
平面![]() ,证明:平面
,证明:平面![]() 平面
平面![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com