
【题目】已知函数![]() .
.
(1)当![]() 时,求不等式
时,求不等式![]() 的解集;
的解集;
(2)若![]() 的图像与
的图像与![]() 轴围成直角三角形,求
轴围成直角三角形,求![]() 的值.
的值.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)分3段去绝对值解不等式组,再求并;
(2)将y=f(x)去绝对值写出分段函数,根据其图象与x轴围成直角三角形,转化为(a﹣1)(a+1)=﹣1或(a+1)(1﹣a)=﹣1,可解得.
(1)当a=2时,不等式f(x)>1,即|x+1|﹣|2x﹣3|>1,
当x≤﹣1时,原不等式可化为﹣x﹣1+2x﹣3>1,解得x>5,因为x≤﹣1,所以此时原不等式无解;
当﹣1![]() 时,原不等式可化为x+1+2x﹣3>1,解得x>1,所以1<x
时,原不等式可化为x+1+2x﹣3>1,解得x>1,所以1<x![]() ;
;
当x![]() 时,原不等式可化为x+1﹣2x+3>1,解得x<3,所以
时,原不等式可化为x+1﹣2x+3>1,解得x<3,所以![]() x<3.
x<3.
综上,原不等式的解集为{x|1<x<3}.
(2)因为![]() ,所以
,所以![]() ,所以
,所以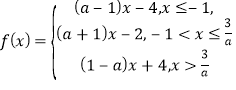 ,
,
因为![]() ,所以
,所以![]() ,
,![]() ,
,
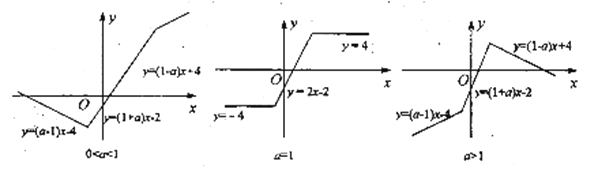
当![]() 时,要使得
时,要使得![]() 的图象与
的图象与![]() 轴围成直角三角形,
轴围成直角三角形,
则![]() ,解得
,解得![]() ,舍去;
,舍去;
当![]() 时,
时,![]() 的图象与
的图象与![]() 轴不能围成三角形,不符合题意,舍去;
轴不能围成三角形,不符合题意,舍去;
当![]() 时,要使得
时,要使得![]() 的图象与
的图象与![]() 轴围成直角三角形,
轴围成直角三角形,
则![]() ,解得
,解得![]() ,因为
,因为![]() ,所以
,所以![]() .
.
综上,所求![]() 的值为
的值为![]() .
.


科目:高中数学 来源: 题型:
【题目】现有长分别为![]() 、
、![]() 、
、![]() 的钢管各3根(每根钢管的质地均匀、粗细相同且富有不同的编号),从中随机抽取
的钢管各3根(每根钢管的质地均匀、粗细相同且富有不同的编号),从中随机抽取![]() 根(假设各钢管被抽取的可能性是均等的,
根(假设各钢管被抽取的可能性是均等的,![]() ),再将抽取的钢管相接焊成笔直的一根.
),再将抽取的钢管相接焊成笔直的一根.
(I)当![]() 时,记事件
时,记事件![]() ,求
,求![]() ;
;
(II)当![]() 时,若用
时,若用![]() 表示新焊成的钢管的长度(焊接误差不计),求
表示新焊成的钢管的长度(焊接误差不计),求![]() 的分布列和数学期望
的分布列和数学期望![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高二奥赛班N名学生的物理测评成绩(满分120分)分布直方图如下,已知分数在100~110的学生数有21人。

(Ⅰ)求总人数N和分数在110~115分的人数n;
(Ⅱ)现准备从分数在110~115分的n名学生(女生占![]() )中任选2人,求其中恰好含有一名女生的概率;
)中任选2人,求其中恰好含有一名女生的概率;
(Ⅲ)为了分析某个学生的学习状态,对其下一阶段的学习提供指导性建议,对他前7次考试的数学成绩x(满分150分),物理成绩y进行分析,下面是该生7次考试的成绩。
数学 | 88 | 83 | 117 | 92 | 108 | 100 | 112 |
物理 | 94 | 91 | 108 | 96 | 104 | 101 | 106 |
已知该生的物理成绩y与数学成绩x是线性相关的,若该生的数学成绩达到130分,请你估计他的物理成绩大约是多少?
附:对于一组数据![]() 其回归线
其回归线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线C的方程为
中,曲线C的方程为![]() .以坐标原点为极点,
.以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线C的参数方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与
与![]() 轴和y轴分别交于A,B两点,P为曲线C上的动点,求△PAB面积的最大值.
轴和y轴分别交于A,B两点,P为曲线C上的动点,求△PAB面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年1月1日,我国全面实行二孩政策,某机构进行了街头调查,在所有参与调查的青年男女中,持“响应”“犹豫”和“不响应”态度的人数如表所示:
响应 | 犹豫 | 不响应 | |
男性青年 | 500 | 300 | 200 |
女性青年 | 300 | 200 | 300 |
(1)根据已知条件完成下面的2×2列联表,并判断能否有97.5%的把握认为犹豫与否与性别有关;
犹豫 | 不犹豫 | 总计 | |
男性青年 |
|
|
|
女性青年 |
|
|
|
总计 |
|
| 1800 |
(2)以表中频率作为概率,若从街头随机采访青年男女各2人,求4人中“响应”的人数恰好是“不响应”的人数(“不响应”的人数不为0)的2倍的概率.
参考公式: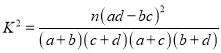
参考数据:
P(K2≥k0) | 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD为矩形,平面PCD⊥平面ABCD,AB=2,BC=1,![]() ,E为PB中点.利用空间向量方法完成以下问题:
,E为PB中点.利用空间向量方法完成以下问题:
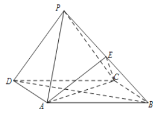
(1)求二面角E-AC-D的余弦值;
(2)在棱PD上是否存在点M,使得![]() ?若存在,求
?若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com