Question

已知集合A={x|（a-1）x²-2x+1=0}并且集合A有且仅有两个子集，求实数a的值及对应的两个子集．

Answer 1

.解：由题意可得 集合A为单元素集
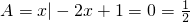
（1）当a=1时 ，此时集合A的两个子集是，∅
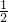
（2）当a≠1时 则△=4-4（a-1）=0解得a=2，此时集合A的两个子集是{1}，∅
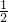
∴实数 a的值是1或2．当a=1时，集合A的两个子集是，∅；当a=2，此时集合A的两个子集是{1}，∅．
分析：若A恰有两个子集，则A为单元素集，所以关于x的方程（a-1）x²-2x+1=0恰有一个实数解，分类讨论能求出实数a的取值范围．
点评：本题考查根据子集与真子集的概念，实数a的取值范围的求法，解题时要认真审题，注意分析法、讨论法和等价转化法的合理运用．