
【题目】某研究性学习小组对春季昼夜温差大小与某花卉种子发芽多少之间的关系进行研究,他们分别记录了3月1日至3月5日的每天昼夜温差与实验室每天100颗种子浸泡后的发芽数,得到如下资料:
K日 日期期 | 1日 | 2日 | 3日 | 4日 | 5日 |
温差x(℃) | 10 | 11 | 13 | 12 | 8 |
发芽数y(颗) | 23 | 25 | 30 | 26 | 16 |
(1)求这5天发芽数的中位数;
(2)求这5天的平均发芽率;
(3)从3月1日至3月5日中任选2天,记前面一天发芽的种子数为m,后面一天发芽的种子数为n,用(m,n)的形式列出所有基本事件,并求满足“![]() ”的概率.
”的概率.
【答案】(1)25;(2) 24%;(3) ![]() .
.
【解析】试题分析:(1)根据中位数概念即可写出.(2)要求种子的平均发芽率,把所有的发芽的种子数相加,除以所有参与实验的种子数,得到发芽的百分率.<BR>(3)由题意知本题是一个古典概型,试验发生包含的事件可以通过列举得到事件数,满足条件的事件也可以在前面列举的基础上得到事件数,根据古典概型概率公式得到结果.
试题解析:(1)因为16<23<25<26<30,所以这5天发芽数的中位数是25.
(2)这5天的平均发芽率为
![]() ×100%=24%.
×100%=24%.
(3)用(x,y)表示所求基本事件,则有
(23,25),(23,30),(23,26),(23,16),(25,30),(25,26),(25,16),(30,26),(30,16),(26,16).共有10个基本事件.
记“![]() ”为事件A,
”为事件A,
则事件A包含的基本事件为(25,30),(25,26),(30,26),共有3个基本事件.所以P(A)=![]() ,即事件“
,即事件“![]() ”的概率为
”的概率为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知正项等比数列{an}满足:a7=a6+2a5 , 若存在两项am , an , 使得 ![]() =4a1 , 则
=4a1 , 则 ![]() +
+ ![]() 的最小值为( )
的最小值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
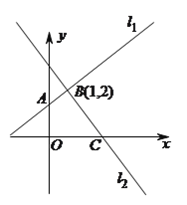
【题目】如图,经过点![]() 作两条互相垂直的直线
作两条互相垂直的直线![]() 和
和![]() ,直线
,直线![]() 交
交![]() 轴正半轴于点
轴正半轴于点![]() ,直线
,直线![]() 交
交![]() 轴正半轴于点
轴正半轴于点![]() .
.
(1)如果![]() ,求点
,求点![]() 的坐标.
的坐标.
(2)试问是否总存在经过![]() ,
, ![]() ,
, ![]() ,
, ![]() 四点的圆?如果存在,求出半径最小的圆的方程;如果不存在,请说明理由.
四点的圆?如果存在,求出半径最小的圆的方程;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为直角坐标系的坐标原点,双曲线
为直角坐标系的坐标原点,双曲线![]()
![]() 上有一点
上有一点![]() (
(![]() ),点
),点![]() 在
在![]() 轴上的射影恰好是双曲线
轴上的射影恰好是双曲线![]() 的右焦点,过点
的右焦点,过点![]() 作双曲线
作双曲线![]() 两条渐近线的平行线,与两条渐近线的交点分别为
两条渐近线的平行线,与两条渐近线的交点分别为![]() ,
, ![]() ,若平行四边形
,若平行四边形![]() 的面积为1,则双曲线的标准方程是( )
的面积为1,则双曲线的标准方程是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. 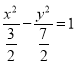
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某年级举办团知识竞赛.![]() 、
、![]() 、
、![]() 、
、![]() 四个班报名人数如下:
四个班报名人数如下:
班别 |
|
|
|
|
人数 | 45 | 60 | 30 | 15 |
年级在报名的同学中按分层抽样的方式抽取10名同学参加竞赛,每位参加竞赛的同学从10个关于团知识的题目中随机抽取4个作答,全部答对的同学获得一份奖品.
(Ⅰ)求各班参加竞赛的人数;
(Ⅱ)若![]() 班每位参加竞赛的同学对每个题目答对的概率均为
班每位参加竞赛的同学对每个题目答对的概率均为![]() ,求
,求![]() 班恰好有2位同学获得奖品的概率;
班恰好有2位同学获得奖品的概率;
(Ⅲ)若这10个题目,小张同学只有2个答不对,记小张答对的题目数为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C的对边分别为a,b,c,且bsinA=![]() acosB.
acosB.
(1)求角B的大小;
(2)若b=3,sinC=2sinA,求a,c的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=1,an= ![]() (n∈N* , n≥2),数列{bn}满足关系式bn=
(n∈N* , n≥2),数列{bn}满足关系式bn= ![]() (n∈N*).
(n∈N*).
(1)求证:数列{bn}为等差数列;
(2)求数列{an}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了丰富退休生活,老王坚持每天健步走,并用计步器记录每天健步走的步数.他从某月中随机抽取20天的健步走步数(老王每天健步走的步数都在![]() 之间,单位:千步),绘制出频率分布直方图(不完整)如图所示.
之间,单位:千步),绘制出频率分布直方图(不完整)如图所示.
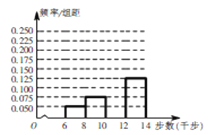
(1)完成频率分布直方图,并估计该月老王每天健步走的平均步数(每组数据可用区间中点值代替;
(2)某健康组织对健步走步数的评价标准如下表:
每天步数分组(千步) |
|
|
|
评价级别 | 及格 | 良好 | 优秀 |
现从这20天中评价级别是“及格”或“良好”的天数里随机抽取2天,求这2天的健步走结果属于同一评价级别的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com