
【题目】已知函数![]() .
.
(1)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)若![]() 有两个零点,求
有两个零点,求![]() 的取值范围.
的取值范围.
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:(1) 求出![]() ,由
,由![]() 可求出切线的斜率,根据点斜式即可求得切线方程;(2)讨论两种情况,当
可求出切线的斜率,根据点斜式即可求得切线方程;(2)讨论两种情况,当![]() 时,显然
时,显然![]() 在
在![]() 上单调递增,至多一个零点,不符合题意,当
上单调递增,至多一个零点,不符合题意,当![]() 时,可证明:当
时,可证明:当![]() 时,
时,![]() 有两个零点.即
有两个零点.即![]() 的取值范围是
的取值范围是![]() .
.![]()
试题解析:(1)![]()
(2)![]()
①当![]() 时,显然
时,显然![]() 在
在![]() 上单调递增;
上单调递增;
②当![]() 时,令
时,令![]() ,则
,则![]() ,易知其判别式为正,
,易知其判别式为正,
设方程的两个根分别为![]() ,则
,则![]() ,
,
![]()
令![]() 得
得![]() ,其中
,其中![]() ,
,
所以函数![]() 在
在![]() 上递增,在
上递增,在![]() 上递减.
上递减.
①当![]() 时,显然
时,显然![]() 在
在![]() 上单调递增,至多一个零点,不符合题意;
上单调递增,至多一个零点,不符合题意;
②当![]() 时,函数
时,函数![]() 在
在![]() 上递增,在
上递增,在![]() 上递减,
上递减,
![]() 要使
要使![]() 有两个零点,必须
有两个零点,必须![]() ,即
,即![]() ,
,
又由![]() 得:
得:![]() ,代入上面的不等式得:
,代入上面的不等式得:
![]() ,解得
,解得![]()
下面证明:当![]() 时,
时,![]() 有两个零点.
有两个零点.
![]() ,
,
![]()
又![]() ,
,
且![]() ,
,
![]() ,
,
所以![]() 在
在![]() 与
与![]() 上各有一个零点.
上各有一个零点.
【方法点晴】本题主要考查利用导数求曲线切线方程、利用导数研究函数的单调性与零点,属于难题.求曲线切线方程的一般步骤是:(1)求出![]() 在
在![]() 处的导数,即
处的导数,即![]() 在点
在点![]()
![]() 出的切线斜率(当曲线
出的切线斜率(当曲线![]() 在
在![]() 处的切线与
处的切线与![]() 轴平行时,在 处导数不存在,切线方程为
轴平行时,在 处导数不存在,切线方程为![]() );(2)由点斜式求得切线方程
);(2)由点斜式求得切线方程![]() .
.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的焦距为2,过短轴的一个端点与两个焦点的圆的面积为
的焦距为2,过短轴的一个端点与两个焦点的圆的面积为![]() ,过椭圆
,过椭圆![]() 的右焦点作斜率为
的右焦点作斜率为![]() (
(![]() )的直线
)的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 、
、![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过点![]() 垂直于
垂直于![]() 的直线与
的直线与![]() 轴交于点
轴交于点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班有36名同学参加数学、物理、化学课外探究小组,每名同学至多参加两个小组,已知参加数学、物理、化学小组的人数分别为26,15,13,同时参加数学和物理小组的有6人,同时参加物理和化学小组的有4人,则同时参加数学和化学小组的有人.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设要抽查某企业生产的某种品牌的袋装牛奶的质量是否达标,现从700袋牛奶中抽取50袋进行检验.利用随机数表抽取样本时,先将700袋牛奶按001,002,…,700进行编号,如果从随机数表第3行第1组数开始向右读,最先读到的5袋牛奶的编号是614,593,379,242,203,请你以此方式继续向右读数,随后读出的3袋牛奶的编号是 . (下列摘取了随机数表第1行至第5行) 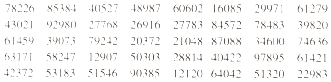
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|x=a0+a1×2+a2×22+a3×23},其中ai∈{0,1,2}(i=0,1,2,3),且a0≠0,则A中所有元素之和等于 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设小明家订了一份报纸,送报人可能在早上6:30﹣7:30之间把报纸送到小明家,小明父亲离开家去工作的时间在早上7:00﹣8:00之间,问小明父亲在离开家前能得到报纸(称为事件A)的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com