
【题目】设f(x)=xex﹣ax2﹣2ax.
(Ⅰ)若y=f(x)的图象在x=﹣1处的切线经过坐标原点,求a的值;
(Ⅱ)若f(x)存在极大值,且极大值小于0,求a的取值范围.
【答案】(Ⅰ)a![]() ;(Ⅱ)(0,
;(Ⅱ)(0,![]() )∪(
)∪(![]() ,
,![]() ).
).
【解析】
(Ⅰ)求f'(x)得到切线斜率,结合直线过原点,即得解;
(Ⅱ)分a≤0,a>0两种情况分析导数极值,得到f(ln2a)是极大值,由极大值小于0,求a的取值范围.
(Ⅰ)f'(x)=ex+xex﹣2ax﹣2a=(x+1)(ex﹣2a),f'(﹣1)=0,f(﹣1)![]() a,
a,
所以由题意得:0 ,∴a
,∴a![]() ;
;
(Ⅱ)由(Ⅰ)得,当2a≤0时,即a≤0时,ex﹣2a≥0,
∴x<﹣1,f'(x)<0,f(x)单调递减,
x>﹣1,f'(x)>0,f(x)单调递增,
所以f(x)有极小值,无极大值;
当a>0,f'(x)=0,x=﹣1或x=ln2a,
当ln2a>﹣1时,即a![]() ,
,
∴x∈(﹣∞,﹣1)和 (ln2a,+∞),f'(x)>0,f(x)单调递增,
当﹣1<x<ln2a时,
f'(x)<0,f(x)单调递减,
所以f(﹣1)为极大值,且f(﹣1)![]() a,由题意得:f(﹣1)<0,∴
a,由题意得:f(﹣1)<0,∴![]() ;
;
当ln2a<﹣1时,即0<a![]() ,
,
∴x∈(﹣∞,ln2a)和 (﹣1,+∞),f'(x)>0,f(x)单调递增,
x∈(ln2a,﹣1),f'(x)<0,f(x)单调递减,
所以f(ln2a)是极大值,且f(ln2a)=2aln2a﹣aln22a﹣2aln2a=﹣aln22a<0恒成立;
当ln2a=﹣1时,即a![]() ,f'(x)=(x+1)2≥0恒成立,f(x)单调递增,无极值,舍去;
,f'(x)=(x+1)2≥0恒成立,f(x)单调递增,无极值,舍去;
综上所述:符合条件的a的取值范围:(0,![]() )∪(
)∪(![]() ,
,![]() ).
).


科目:高中数学 来源: 题型:
【题目】已知某产品的历史收益率的频率分布直方图如图所示.
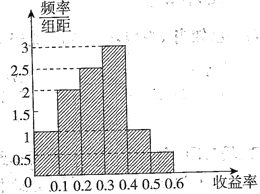
(1)试估计该产品收益率的中位数;
(2)若该产品的售价![]() (元)与销量
(元)与销量![]() (万份)之间有较强线性相关关系,从历史销售记录中抽样得到如表5组
(万份)之间有较强线性相关关系,从历史销售记录中抽样得到如表5组![]() 与
与![]() 的对应数据:
的对应数据:
售价 | 25 | 30 | 38 | 45 | 52 |
销量 | 7.5 | 7.1 | 6.0 | 5.6 | 4.8 |
根据表中数据算出![]() 关于
关于![]() 的线性回归方程为
的线性回归方程为![]() ,求
,求![]() 的值;
的值;
(3)若从表中五组销量数据中随机抽取两组,记其中销量超过6万份的组数为![]() ,求
,求![]() 的分布列及期望.
的分布列及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点![]() 到定直线
到定直线![]() :
:![]() 的距离比到定点
的距离比到定点![]() 的距离大2.
的距离大2.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)在![]() 轴正半轴上,是否存在某个确定的点
轴正半轴上,是否存在某个确定的点![]() ,过该点的动直线
,过该点的动直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,使得
两点,使得![]() 为定值.如果存在,求出点
为定值.如果存在,求出点![]() 坐标;如果不存在,请说明理由.
坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy下,曲线C1的参数方程为![]() (
(![]() 为参数),曲线C1在变换T:
为参数),曲线C1在变换T:![]() 的作用下变成曲线C2.
的作用下变成曲线C2.
(1)求曲线C2的普通方程;
(2)若m>1,求曲线C2与曲线C3:y=m|x|-m的公共点的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
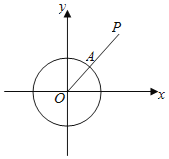
【题目】在平面直角坐标系xOy中,对于⊙O:x2+y2=1来说,P是坐标系内任意一点,点P到⊙O的距离SP的定义如下:若P与O重合,SP=r;若P不与O重合,射线OP与⊙O的交点为A,SP=AP的长度(如图).
(1)直线2x+2y+1=0在圆内部分的点到⊙O的最长距离为_____;
(2)若线段MN上存在点T,使得:
①点T在⊙O内;
②点P∈线段MN,都有ST≥SP成立.则线段MN的最大长度为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项数列![]() 满足:
满足:![]() ,
,![]() ,其中
,其中![]() .
.
(1)若![]() ,求数列
,求数列![]() 的前
的前![]() 项的和;
项的和;
(2)若![]() ,
,![]() .
.
①求数列![]() 的通项公式;
的通项公式;
②记数列![]() 的前
的前![]() 项的和为
项的和为![]() ,若无穷项等比数列
,若无穷项等比数列![]() 始终满足
始终满足![]() ,求数列
,求数列![]() 的通项公式.
的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知{an}是等差数列,其前n项和Sn=n2﹣2n+b﹣1,{bn}是等比数列,其前n项和Tn![]() ,则数列{ bn +an}的前5项和为( )
,则数列{ bn +an}的前5项和为( )
A.37B.-27C.77D.46
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的离心率为
的离心率为![]() ,左、右顶点分别为A,B,点M是椭圆C上异于A,B的一点,直线AM与y轴交于点P.
,左、右顶点分别为A,B,点M是椭圆C上异于A,B的一点,直线AM与y轴交于点P.
(Ⅰ)若点P在椭圆C的内部,求直线AM的斜率的取值范围;
(Ⅱ)设椭圆C的右焦点为F,点Q在y轴上,且∠PFQ=90°,求证:AQ∥BM.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为抗击新型冠状病毒,普及防护知识,某校开展了“疫情防护”网络知识竞赛活动.现从参加该活动的学生中随机抽取了100名学生,将他们的比赛成绩(满分为100分)分为6组:![]() ,得到如图所示的频率分布直方图.
,得到如图所示的频率分布直方图.
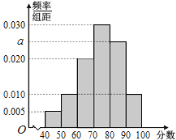
(1)求![]() 的值,并估计这100名学生的平均成绩(同一组中的数据用该组区间的中点值为代表);
的值,并估计这100名学生的平均成绩(同一组中的数据用该组区间的中点值为代表);
(2)在抽取的100名学生中,规定:比赛成绩不低于80分为“优秀”,比赛成绩低于80分为“非优秀”.请将下面的2×2列联表补充完整,并判断是否有99%的把握认为“比赛成绩是否优秀与性别有关”?
优秀 | 非优秀 | 合计 | |
男生 | 40 | ||
女生 | 50 | ||
合计 | 100 |
参考公式及数据:![]() .
.
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com