某少数民族的刺绣有着悠久的历史，如图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案，这些图案都是由小正方形构成，小正方形数越多刺绣越漂亮．现按同样的规律刺绣(小正方形的摆放规律相同)，设第n个图形包含f(n)个小正方形．
(1)求出f(5)的值；
(2)利用合情推理的“归纳推理思想”，归纳出f(n＋1)与f(n)之间的关系式，并根据你得到的关系式求出f(n)的表达式；
(3)求
＋
＋
＋…＋
的值．
科目：高中数学 来源： 题型：解答题
已知二次函数f(x)＝ax2＋bx＋c的图象与x轴有两个不同的交点，若f(c)＝0且0<x<c时，f(x)>0，
(1)证明：
是f(x)＝0的一个根；
(2)试比较与c的大小；
(3)证明：－2<b<－1.
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
如图所示,底面为平行四边形ABCD的四棱锥P-ABCD中,E为PC的中点.求证:PA∥平面BDE.(要求注明每一步推理的大前提、小前提和结论,并最终把推理过程用简略的形式表示出来)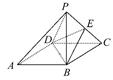
查看答案和解析>>
科目：高中数学 来源： 题型：填空题
从装有
个球（其中
个白球，1个黑球）的口袋中取出
个球（
），共有
种取法，在这种取法中，可以分为两类：一类是取出的个球全部为白球，另一类是取出的m个球中有1个黑球，共有
种取法，即有等式：
成立.
试根据上述思想化简下列式子：
_____
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
－
.
，使等式
对于一切
都成立？若不存在，说明理由；若存在，请用数学归纳法证明？
，则
(
)
均为实数，且
，
，
求证：
，
，
，……